Refine search
Actions for selected content:
28957 results in Differential and integral equations, dynamical systems and control theory
A note on summability factors
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-40
- Print publication:
- June 1957
-
- Article
- Export citation
MTK volume 4 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f3
- Print publication:
- June 1957
-
- Article
-
- You have access
- Export citation
The Green's function of an elliptic plate
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 61-69
- Print publication:
- June 1957
-
- Article
- Export citation
XVIII.—Recent Oceanographical Investigations in the Faroe-Shetland Channel*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 3 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 239-289
- Print publication:
- 1957
-
- Article
- Export citation
XIX.—Metrisable Lie Groups and Algebras
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 3 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 290-304
- Print publication:
- 1957
-
- Article
- Export citation
XXI.—Index Polynomials and Bifurcating Root-Trees*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 4 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 319-341
- Print publication:
- 1957
-
- Article
- Export citation
PRM volume 64 issue 3 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 3 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f2
- Print publication:
- 1957
-
- Article
-
- You have access
- Export citation
XXIV.—Conditions for the Ergodicity of Non-homogeneous Finite Markov Chains*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 4 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 369-380
- Print publication:
- 1957
-
- Article
- Export citation
XX.—On the Theory of Binary Fluid Mixtures
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 3 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 305-317
- Print publication:
- 1957
-
- Article
- Export citation
XXII.—On Methods of Summability Based on Power Series*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 4 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 342-349
- Print publication:
- 1957
-
- Article
- Export citation
XXV.—The Determination of Temperature Gradients over the Greenland Ice Sheet by Optical Methods
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 4 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 381-397
- Print publication:
- 1957
-
- Article
- Export citation
XXIII. —Marine Research—The Work of the National Institute of Oceanography
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 4 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 350-368
- Print publication:
- 1957
-
- Article
- Export citation
PRM volume 64 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 4 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f2
- Print publication:
- 1957
-
- Article
-
- You have access
- Export citation
XVII.—Invariant Matrices and the Geometry of Numbers
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 3 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 223-238
- Print publication:
- 1957
-
- Article
- Export citation
Index
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 4 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. 399-401
- Print publication:
- 1957
-
- Article
- Export citation
PRM volume 64 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 4 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b7
- Print publication:
- 1957
-
- Article
-
- You have access
- Export citation
PRM volume 64 issue 3 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 64 / Issue 3 / 1957
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b2
- Print publication:
- 1957
-
- Article
-
- You have access
- Export citation
Solution of the Word Problem for Certain Types of Groups I
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 3 / Issue 1 / December 1956
- Published online by Cambridge University Press:
- 18 May 2009, pp. 45-54
- Print publication:
- December 1956
-
- Article
-
- You have access
- Export citation
The spread of a matrix
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-130
- Print publication:
- December 1956
-
- Article
- Export citation
Dilational and distortional vibrations of semi-infinite solids and plates
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 153-163
- Print publication:
- December 1956
-
- Article
- Export citation
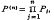 where
where 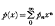 with real non-negative coefficients and having radius of convergence
with real non-negative coefficients and having radius of convergence