In its simplest form, the theorem of Ascoli with which we are concerned is an extension of the Bolzano-Weierstrass theorem: it states that, if X and Y are bounded closed sets, of real or complex numbers, andis a sequence of equicontinuous functions mapping X into Y, thenhas a uniformly convergent subsequence. As is well known, this result has played a fundamental part in the development of several theories; it has also been widely generalized, by processes of abstraction and localization, and a very useful version of the theorem runs as follows (cf. [4], 233–234):

(A) Suppose that X is a locally compact regular space, and that Y is a Hausdorff space whose topology is determined by a uniform structure. Let YX be the space of all functions that map X into Y, with the topology of locally uniform convergence with respect to. Then a closed setin YX is compact if, at each point x of X, (i) the set(x) is relatively compact, in Y, and, (ii) is equicontinuous with respect to.

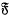
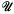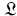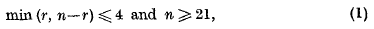
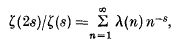
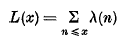
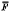The commutative and entropic congruence relations determine a homomorphism on the free logarithmetic , the arithmetic of the indices of powers of the generating element of a free cyclic groupoid. A necessary and sufficient condition that two indices should be concordant (i.e. congruent in the free commutative entropic logarithmetic) is that the bifurcating trees corresponding to these indices should have the same number of free ends at each altitude. It follows that the free commutative entropic logarithmetic can be represented faithfully by index ψ-polynomials (or θ-polynomials) in one indeterminate.

In the concluding section enumeration formulæ are obtained for the number of non-concordant indices of a given altitude and for the number of indices concordant to a given index.

The distribution of xn, the number of occurrences of a given one of k possible states of a non-homogeneous Markov chain {Pj} in n successive trials, is considered. It is shown that if Pn → P, a positive-regular stochastic matrix, as n → ∞ then the distribution about its mean of xn/n½ tends to normality, and that the variance tends to that of the corresponding distribution associated with the homogeneous chain {P}.

The presence of a non-uniform distribution of temperature in an elastic solid gives rise to an additional term in the generalized Hooke's Law connecting the stress and strain tensors and to a term involving the time rate of change of the dilatation in the equation governing the conduction of heat in the solid. The present paper is concerned with the effects produced by these additional terms in two simple situations. In the first, the elastic solid is regarded as being of infinite extent and the distribution of temperature in the solid is produced by heat sources whose strength may vary with time. In the second, the solid is supposed to be semi-infinite and to be deformed by prescribed variations in the temperature of the bounding plane and by heat sources within itself.

If the temperature in an elastic rod is not uniform and if it varies with time, dynamic thermal stresses are set up in the rod. This paper is concerned with the calculation of the distribution of temperature and stress in an elastic rod when its ends are subjected to mechanical or thermal disturbances. Simple waves in an infinite rod are first discussed and then boundary value problems for semi-infinite rods and rods of finite length. The paper concludes with an account of an approximate method of solving the equations of thermoelasticity.

The roots of the equation zez = a are of importance in several theories. Various authors have studied certain of their properties over more than a century. Here we solve the equation, in the sense that we define the sequence {Zn} of roots and, except for a small, finite number of values of n, find a rapidly convergent series for Zn. The terms in this series are alternately real and purely imaginary and so the series is very convenient for calculation. For the few remaining roots, we give practicable methods of numerical calculation and supply an auxiliary table.

The main results of this article have been announced without proof or details in Wright 1959.

Let Q(x1 …, xn) be an indefinite quadratic form in n variables with real coefficients. Suppose that when Q is expressed as a sum of squares of real linear forms, with positive and negative signs, there are r positive signs and n—r negative signs. It was proved recently by Birch and Davenport that, if

then for any ε > 0 the inequality

is soluble in integers x1, …, xn, not all 0.

Let λ(n) be Liouville's function denned by

where v is the number of prime factors of n, repeated factors being counted according to their multiplicity. Alternatively, λ(n) may be denned by the relation

where ζ(s) is the zeta function of Riemann.

Let Q be a complete local ring which has the same characteristic as its residue field P, and, for the present, let us denote by A the image of a subset A of Q under the natural homomorphism of Q onto P. Then a subfield F of Q is called a coefficient field if = P. It has been shown in [2] and in [3] that a complete equicharacteristic local ring, such as the above, always possesses at least one coefficient field; this is the embedding theorem for the equicharacteristic case.

Given a series we define , by the relations

The series is said to be summable (C, k), where k > - 1, to the sum s if

to be summable (C, - 1) to s if it converges to s and nan = o(l); to be absolutely summable (C, k), or summable | C, k, to s if it is summable (C, k) to s and

and to be strongly Cesàro summable to s with order k > 0 and index p or summable [C; k, p] to s, if

In a recent paper [1], the author divided the semi-special permutations on [n] that are not linear into two classes. The first class consists of the semi-special permutations which, for all possible values of s, have s as a principal number and which induce modulo s the identity permutation. The second class consists of all the semi-special permutations, with principal number s, which induce modulo s linear permutations other than the identity, where again s takes all its possible values.

The following work establishes a new proof of the theorem: Every archimedean ordered group is abelian. This theorem has been proved differently by many authors. It was first proved by O. Hölder [2]. A second proof has been given by H. Cartan [1]: he uses the topology which is naturally introduced in the group by its order.

All operators considered in this paper are bounded and linear (everywhere defined) on a Hilbert space. An operator A will be called a square root of an operator B if

A simple sufficient condition guaranteeing that any solution A of (1) be normal whenever B is normal was obtained in [1], namely: If B is normal and if there exists some real angle θ for which Re(Aeιθ)≥0, then (1) implies that A is normal. Here, Re (C) denotes the real part ½(C + C*) of an operator C.

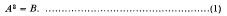
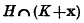If K is a convex body in n-dimensional space, let SK denote the closed n-dimensional sphere with centre at the origin and with volume equal to that of K. If H and K are two such convex bodies let C(H, K) denote the least convex cover of the union of H and K, and let V*(H, K) denote the maximum, taken over all points x for which the intersection is not empty, of the volume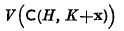

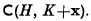of the set . The object of this paper is to discuss some of the more interesting consequences of the following general theorem.

The present paper is an attempt to develop and illuminate the foundations of structure theory as presented in a previous paper [8] which will be referred to as I.

Our approach is based on an unorthodox view of physical theory, largely due to Eddington ([5], [6], [7]), that leads us to expect that at least some (and perhaps all) physical laws are derivable from a consideration of the intrinsic nature of measurement. This is discussed in the Introduction of I. A theory with this approach will be called “pre-empirical”, in contrast with orthodox physical theories, which are postempirical.