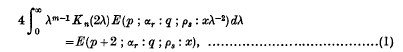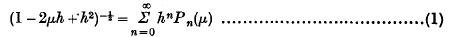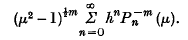Refine search
Actions for selected content:
28953 results in Differential and integral equations, dynamical systems and control theory
Generalisations of Some Hypergeometric Function Transformations
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. 38-41
- Print publication:
- January 1952
-
- Article
-
- You have access
- Export citation
XXVI.—The Normal Penetration of a Thin Elastic-Plastic Plate by a Right Circular Cone*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 4 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 359-370
- Print publication:
- 1952
-
- Article
- Export citation
XV.—Theorems on the Convergence and Asymptotic Validity of Abel's Series*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 3 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 222-231
- Print publication:
- 1952
-
- Article
- Export citation
GMJ volume 1 issue 1 Cover and Back matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- January 1952
-
- Article
-
- You have access
- Export citation
XXIX.—The First Chemical Society, the First Chemical Journal, and the Chemical Revolution (Part II)*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 4 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 385-400
- Print publication:
- 1952
-
- Article
- Export citation
XXII.—Artificial Holograms and Astigmatism*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 4 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 313-323
- Print publication:
- 1952
-
- Article
- Export citation
On Neumann's Formula for the Legendre Functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. 10-12
- Print publication:
- January 1952
-
- Article
-
- You have access
- Export citation
XXVII.—The Rotational Field behind a Bow Shock Wave in Axially Symmetric Flow using Relaxation Methods*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 4 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 371-380
- Print publication:
- 1952
-
- Article
- Export citation
XX.—On the Estimation of Variance and Covariance
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 3 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 280-289
- Print publication:
- 1952
-
- Article
- Export citation
Addendum
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 4 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 323-325
- Print publication:
- 1952
-
- Article
- Export citation
XXV.—The First Chemical Society, the First Chemical Journal, and the Chemical Revolution*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 4 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 346-358
- Print publication:
- 1952
-
- Article
- Export citation
XXVIII.—A Molecular Sum Rule*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 4 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 381-384
- Print publication:
- 1952
-
- Article
- Export citation
An Integral Involving the Product of a Bessel Function and an E-Function
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. 8-9
- Print publication:
- January 1952
-
- Article
-
- You have access
- Export citation
XXIII.—Studies in Practical Mathematics. VII. On the Theory of Methods of Factorizing Polynomials by Iterated Division*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 4 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 326-335
- Print publication:
- 1952
-
- Article
- Export citation
XIV.—Experiments in Diffraction Microscopy*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 3 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 193-221
- Print publication:
- 1952
-
- Article
- Export citation
XVII.—The Sargent Diagram for the Electron-capture Process, and the Disintegration Energies of Heavy β-emitters*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 3 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 242-256
- Print publication:
- 1952
-
- Article
- Export citation
Integrals of Lommel's Type for Confluent Hypergeometric Functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. 28-31
- Print publication:
- January 1952
-
- Article
-
- You have access
- Export citation
An Expansion in Terms of Associated Legendre Functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. 13-15
- Print publication:
- January 1952
-
- Article
-
- You have access
- Export citation
GMJ volume 1 issue 1 Cover and Front matter
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f7
- Print publication:
- January 1952
-
- Article
-
- You have access
- Export citation
XVI.—Some Continuant Determinants arising in Physics and Chemistry—II*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 3 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 232-241
- Print publication:
- 1952
-
- Article
- Export citation




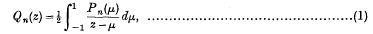
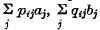 respectively. The
respectively. The