Refine search
Actions for selected content:
28953 results in Differential and integral equations, dynamical systems and control theory
XXI.—The Statistical Theory of Stiff Chains
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 3 / 1952
- Published online by Cambridge University Press:
- 14 February 2012, pp. 290-311
- Print publication:
- 1952
-
- Article
- Export citation
Note on the Strong Summability of Series
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. 16-20
- Print publication:
- January 1952
-
- Article
-
- You have access
- Export citation
Solutions of the Diffusion Equation for a Medium Generating Heat
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. 21-27
- Print publication:
- January 1952
-
- Article
-
- You have access
- Export citation
Inequalities for a Class of Terminating Generalised Hypergeometric Functions
-
- Journal:
- Proceedings of the Glasgow Mathematical Association / Volume 1 / Issue 1 / January 1952
- Published online by Cambridge University Press:
- 18 May 2009, pp. 32-37
- Print publication:
- January 1952
-
- Article
-
- You have access
- Export citation
XIII.—Studies in Practical Mathematics. VI. On the Factorization of Polynomials by Iterative Methods*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 2 / 1951
- Published online by Cambridge University Press:
- 14 February 2012, pp. 174-191
- Print publication:
- 1951
-
- Article
- Export citation
XII.—Clebsch-Aronhold Symbols and the Theory of Symmetric Functions*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 2 / 1951
- Published online by Cambridge University Press:
- 14 February 2012, pp. 155-173
- Print publication:
- 1951
-
- Article
- Export citation
XI.—Application of Relaxation Methods to Compressible Flow past a Double Wedge*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 2 / 1951
- Published online by Cambridge University Press:
- 14 February 2012, pp. 139-154
- Print publication:
- 1951
-
- Article
- Export citation
X.—The Reciprocity Theory of Electrodynamics*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 2 / 1951
- Published online by Cambridge University Press:
- 14 February 2012, pp. 105-138
- Print publication:
- 1951
-
- Article
- Export citation
VII.—Parallel Planes in a Riemannian Vn
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 1 / 1950
- Published online by Cambridge University Press:
- 14 February 2012, pp. 78-92
- Print publication:
- 1950
-
- Article
- Export citation
II.—The Stability of Solutions of Non-linear Difference-differential Equations*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 1 / 1950
- Published online by Cambridge University Press:
- 14 February 2012, pp. 18-26
- Print publication:
- 1950
-
- Article
- Export citation
V.—Les transformations asymptotiquement presque périodiques discontinues et le lemme ergodique. (Première Note.)
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 1 / 1950
- Published online by Cambridge University Press:
- 14 February 2012, pp. 61-68
- Print publication:
- 1950
-
- Article
- Export citation
IV.—Studies in Practical Mathematics. V. On the Iterative Solution of a System of Linear Equations*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 1 / 1950
- Published online by Cambridge University Press:
- 14 February 2012, pp. 52-60
- Print publication:
- 1950
-
- Article
- Export citation
VI.—Unbiased Statistics with Minimum Variance
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 1 / 1950
- Published online by Cambridge University Press:
- 14 February 2012, pp. 69-77
- Print publication:
- 1950
-
- Article
- Export citation
IX.—A Measurement of the Velocity of Light*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 1 / 1950
- Published online by Cambridge University Press:
- 14 February 2012, pp. 95-104
- Print publication:
- 1950
-
- Article
- Export citation
PRM volume 63 issue 1 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 1 / 1950
- Published online by Cambridge University Press:
- 14 February 2012, pp. f1-f4
- Print publication:
- 1950
-
- Article
-
- You have access
- Export citation
PRM volume 63 issue 1 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 1 / 1950
- Published online by Cambridge University Press:
- 14 February 2012, pp. b1-b2
- Print publication:
- 1950
-
- Article
-
- You have access
- Export citation
III.—The Simplest Form of Second-Order Linear Differential Equation, with Periodic Coefficient, having Finite Singularities*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 1 / 1950
- Published online by Cambridge University Press:
- 14 February 2012, pp. 27-51
- Print publication:
- 1950
-
- Article
- Export citation
I.—The Adventures of an Hypothesis*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 1 / 1950
- Published online by Cambridge University Press:
- 14 February 2012, pp. 1-17
- Print publication:
- 1950
-
- Article
- Export citation
VIII.—A Further Note on a Problem in Factor Analysis*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 63 / Issue 1 / 1950
- Published online by Cambridge University Press:
- 14 February 2012, pp. 93-94
- Print publication:
- 1950
-
- Article
- Export citation
XLV.—The Internal and External Fields of a Particle in a Gravitational Field
-
- Journal:
- Proceedings of the Royal Society of Edinburgh Section A: Mathematical and Physical Sciences / Volume 62 / Issue 4 / 1949
- Published online by Cambridge University Press:
- 14 February 2012, pp. 427-433
- Print publication:
- 1949
-
- Article
- Export citation
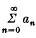 ,the
,the 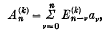
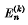 is the binomial coefficient
is the binomial coefficient 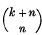 . Let
. Let 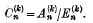 Then Σ
Then Σ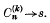 The series is said to be absolutely summable (
The series is said to be absolutely summable (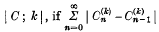 is convergent. The series is said to be strongly summable (
is convergent. The series is said to be strongly summable (