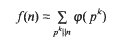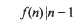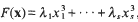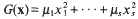Refine search
Actions for selected content:
9018 results in Discrete Mathematics, Information Theory and Coding
How to realize a given number of tangents to four unit balls in ℝ3
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-62
- Print publication:
- December 2001
-
- Article
- Export citation
A syntactic approach to covers for E-dense semigroups over group varieties
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 231-245
- Print publication:
- December 2001
-
- Article
- Export citation
Index to Volume 47
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 July 2012, p. 317
- Print publication:
- December 2001
-
- Article
- Export citation
Lattice points in lattice polytopes
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 15-24
- Print publication:
- December 2001
-
- Article
- Export citation
Deterministic and randomized polynomial-time approximation of radii
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-105
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
The arithmetic of partitions into distinct parts
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 203-211
- Print publication:
- December 2001
-
- Article
- Export citation
The inverse Goldbach problem
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 151-158
- Print publication:
- December 2001
-
- Article
- Export citation
Book Reviews - M. Aigner and G. M. Ziegler. Proofs from The Book (2nd edition). Springer (Berlin), 2001; 215 pp. ISBN 3 540 67865 4 (hardback), £18.50. - R. P. Agarwal M. Meehan and D. O'reagan. Fixed Point Theory and Applications. Cambridge Tracts in Mathematics 141, Cambridge University Press, 2001; 170 pp. ISBN 0 521 80250 4 (hardback), £37.50. - S. Alpern and V. S. Prasad. Typical Dynamics of Volume-Preserving Homeomorphisms. Cambridge Tracts in Mathematics 139, Cambridge University Press, 2000; 216 pp. ISBN 0 521 58287 3 (hardback), £30. - I. Anderson. A First Course in Discrete Mathematics. Springer Undergraduate Mathematics Series, Springer (London), 2000; 200 pp. ISBN 1 85233 236 0 (paperback), £18.95. - M. Aschbacher. Finite Group Theory (2nd edition). Cambridge Studies in Advanced Mathematics 19, Cambridge University Press, 2000; 304 pp. ISBN 0 521 78145 0 (hardback), £52.50; 0 521 78675 4 (paperback), £19.95. - J. Bang-Jensen and G. Gutin. Digraphs: Theory, Algorithms and Applications. Springer Monographs in Mathematics, Springer (London), 2001; 754 pp. ISBN 1 85233 268 9 (hardback), £59. - D. Bao S.-S. Chern and Z. Shen. An Introduction to Riemann-Finsler Geometry. Graduate Texts in Mathematics 200, Springer (New York, Berlin), 2000; 431 pp. ISBN 0 387 98948 X (hardback), £34. - H. Bass and A. Lubotzky. Tree Lattices. Progress in Mathematics 176, Birkhäuser (Boston), 2000; 233 pp. ISBN 0 8176 4120 3 (hardback), £36 (approx.). - V. I. Bernik and M. M. Dobson. Metric Diophantine Aproximation on Manifolds. Cambridge University Press, 1999; 172 pp. ISBN 0 521 43275 8 (hardback), £27.50. - S. Billey and V. Lakshmibai. Singular Loci of Schubert Varieties. Progress in Mathematics 182, Birkhäuser (Boston), 2000; 251 pp. ISBN 0 8176 4092 4 (hardback), £40 (approx.). - F. Borceux and G. Janelidze. Galois Theories. Cambridge Studies in Advanced Mathematics, Cambridge University Press, 2001; 341 pp. ISBN 0 521 80309 8 (hardback), £50. - TH. Breuer. Characters and Automorphism Groups of Compact Riemann Surfaces. London Mathematical Society Lecture Notes Series 280, Cambridge University Press, 2000; 199 pp. ISBN 0 521 79809 4 (paperback), £24.95. - X. H. Cao S. X. Liu K. P. Shum and C. C. Yang. Rings, Groups and Algebras. Lecture Notes in Pure and Applied Mathematics 181, Marcel Dekker, Inc. (New York), 1996; 332 pp. ISBN 0 8247 9733 7 (paperback), £110 (approx.). - E. Casas-Alvero. Singularities of Plane Curves. London Mathematical Society Lecture Notes Series 276, Cambridge University Press, 2000; 345 pp. ISBN 0 521 78959 1 (paperback), £29.95. - J. L. Casti. Five More Golden Rules: Knots, Codes, Chaos and Other Great Theories of 20th Century Mathematics. John Wiley and Sons (New York), 2000; 268 pp. ISBN 0 471 39528 5 (paperback), £12.50. - J. W. Cholewa and T. Dlotko. Global Attractors in Abstract Parabolic Problems. London Mathematical Society Lecture Notes Series 278, Cambridge University Press, 2000; 235 pp. ISBN 0 521 79424 2 (paperback), £27.95. - S. Dăscălescu C. Năstăcescu and Ş Raianu. Hopf Algebras: An Introduction. Monographs and Textbooks in Pure and Applied Mathematics 235, Marcel Dekker, Inc. (New York), 2001; 401 pp. ISBN 0 8247 0481 9 (hardback), £97.40. - K. Deb. Multi-Objective Optimization Using Evolutionary Algorithms. Wiley-Interscience Series in Systems and Optimization, John Wiley and Sons (New York), 2001; 497 pp. ISBN 0 471 87339 X (hardback), £60. - R. A. De Vore A. Iserles and E. Süli. Foundations of Computational Mathematics. London Mathematical Society Lecture Notes Series 284, Cambridge University Press, 2001; 400 pp. ISBN 0 521 00349 0 (paperback), £34.95. - A. K. Dewdney. A Mathematical Mystery Tour. John Wiley and Sons (New York), 1999; 218 pp. ISBN 0 471 23847 3 (paperback), £11.50. - V. Drensky A. Giambruno and S. Sehgal (EDITORS). Methods in Ring Theory. Lecture Notes in Pure and Applied Mathematics 198, Marcel Dekker, Inc. (New York), 1998; 314 pp. ISBN 0 8247 0183 6 (paperback), £95 (approx.). - C. F. Dunkl and Y. Xu. Orthogonal Polynomials of Several Variables. Encyclopedia of Mathematics and its Applications 81, Cambridge University Press, 2001; 390 pp. ISBN 0 521 80043 9 (hardback), £55. - B. Engquist and W. Schmid (EDITORS). Mathematics Unlimited–2001 and Beyond. Springer (Berlin), 2001; 1297 pp. ISBN 3 540 66913 2 (hardback), £27. - D. R. Farenick. The Algebra of Linear Transformations. Springer Universitext, Springer (Berlin), 2001; 238 pp. ISBN 0 387 95062 1 (hardback), £34. - A. T. Filippov. The Versatile Soliton. Birkhäuser (Boston), 2000; 261 pp. ISBN 0 8176 3635 8 (hardback), £32 (approx.). - B. Fine and G. Rosenberger. Algebraic Generalizations of Discrete Groups. Monographs and Textbooks in Pure and Applied Mathematics 223, Marcel Dekker, Inc. (New York), 1999; 317 pp. ISBN 0 8247 0319 7 (hardback). - C. G. Gibson. Elementary Geometry of Differentiable Curves. Cambridge University Press, 2001; 216 pp. ISBN 0 521 80453 (hardback), £47.50; 0 521 01107 8 (paperback), £16.95. - J. J. Gray. Linear Differential Equations and Group Theory from Riemann to Poincaré (2nd edition). Birkhäuser (Basel), 2000; 338 pp. ISBN 0 8176 3837 7 (hardback), £50 (approx.). - E. Győri and V. T. Sős (EDITORS). Recent Trends in Combinatorics: The Legacy of Paul Erőds. Cambridge University Press, 2001; 192 pp. ISBN 0 521 80170 2 (hardback), £35. - D. R. Hankerson D. G. Hoffman D. A. Leonard C. C. Lindner K. T. Phelps C. A. Rodger and J. R. Wall. Coding Theory and Cryptography: The Essentials (2nd edition). Monoographs and Textbooks in Pure and Applied Mathematics 234, Marcel Dekker, Inc. (New York), 2000; 350 pp. ISBN 0 8247 0465 7 (hardback), £60 (approx.). - J. W. P. Hirschfeld (EDITOR). Surveys in Combinatorics 2001. London Mathematical Society Lecture Notes Series 288, Cambridge University Press, 2001; 301 pp. ISBN 0 521 00270 2 (paperback), £27.95. - R. J. IorioJr and V. De M. Iorio. Fourier Analysis and Partial Differential Equations. Cambridge Studies in Advanced Mathematics 70, Cambridge University Press, 2001; 411 pp. ISBN 0 521 62116 X (hardback), £45. - G. Kalai and G. M. Ziegler (EDITORS). Poly topes—Combinatorics and Computation. Birkhäuser (Basel), 2000; 225 pp. ISBN 3 7643 6351 7 (paperback), £20 (approx.). - J. Kigami. Analysis on Fractals. Cambridge Tracts in Mathematics 143, Cambridge University Press, 2001; 226 pp. ISBN 0 521 79321 1 (hardback), £35. - M. Kreuzer and L. Robbiano. Computational Commutative Algebra, I. Springer (Berlin-Heidelberg), 2000; 321 pp. ISBN 3 540 67733 X (hardback), £24. - S. Lang. Collected Papers. Springer (Berlin), 2000 (I-IV), 2001 (V). I: 525 pp. ISBN 0 387 98802 5 (hardback), £55; II: 590 pp. ISBN 0 387 98803 3 (hardback), £55; III: 393 pp. ISBN 0 387 98800 9 (hardback), £55; IV: 471 pp. ISBN 0 387 98804 1 (hardback), £55; V: 426 pp. ISBN 0 387 95030 3 (hardback), £61.50. - J. M. Lee. Introduction to Topological Manifolds. Graduate Texts in Mathematics 202, Springer (Berlin), 2000; 385 pp. ISBN 0 387 98759 2 (hardback), £48; 0 387 95026 5 (paperback), £24. - P. Mayberry. The Foundations of Mathematics in the Theory of Sets. Encyclopedia of Mathematics and its Applications 82, Cambridge University Press, 2000; 424 pp. ISBN 0 521 77034 3 (hardback), £55. - V. V. Mitin D. A. Romanov and M. P. Polis. Modern Advanced Mathematics for Engineers. John Wiley and Sons (New York), 2001; 308 pp. ISBN 0 471 41770 X (hardback), £64.50. - W. F. Pfeffer. Derivation and Integration. Cambridge Tracts in Mathematics 140, Cambridge University Press, 2001; 266 pp. ISBN 0 521 79268 1 (hardback), £45. - A. Pressley. Elementary Differential Geometry. Springer Undergraduate Mathematics Series, Springer (London), 2001; 332 pp. ISBN 1 85233 152 6 (paperback), £18.95. - H. Rademacher and O. Toeplitz. Von Zahlen und Figuren (reprint of the 2nd edition, 1933). Springer (Berlin), 2001; 173 pp. ISBN 3 540 63303 0 (hardback), £25.50. - A. M. Robert. A Course in p-adic Analysis. Springer Graduate Texts in Mathematics 198, Springer (New York, Berlin), 2000; 437 pp. ISBN 0 387 98669 3 (hardback), £37.50. - J. Robinson. Infinite-Dimensional Dynamical Systems. Cambridge Texts in Applied Mathematics, Cambridge University Press, 2001; 461 pp. ISBN 0 521 63204 8 (hardback), £70; 0 521 63564 0 (paperback), £24.95. - G. Sapiro. Geometric Partial Differential Equations and Image Analysis. Cambridge University Press, 2001; 385 pp. ISBN 0 521 79075 1 (hardback). £40. - R. Y. Sharp. Steps in Commutative Algebra (2nd edition). London Mathematical Society Student Texts 51, Cambridge University Press, 2000; 355 pp. ISBN 0 521 64623 5 (paperback), £17.95. - K. E. Smith L. Kahanpaa P. Kekalainen and W. Treves. An Invitation to Algebraic Geometry. Springer Universitext, Springer (New York, Berlin), 2000; 155 pp. ISBN 0 387 98980 3 (hardback), £22. - H. P. F. Swinnerton-Dyer. A Brief Guide to Algebraic Number Theory. London Mathematical Society Student Texts 50, Cambridge University Press, 2001; 146 pp. ISBN 0 521 80292 X (hardback), £45; 0 521 00423 3 (paperback), £15.95. - Y. Talpaert. Differential Geometry with Applications to Mechanics and Physics. Monographs and Textbooks in Pure and Applied Mathematics 237, Marcel Dekker, Inc. (New York), 2001; 454 pp. ISBN 0 8247 0385 5 (hardback), £120 (approx.). - W. T. Tutte. Graph Theory. Cambridge Mathematical Library, Cambridge University Press, 2001; 333 pp. ISBN 0 521 79489 7 (paperback), £19.95. - F. Van Oystaeyen and M. Saorin (EDITORS). Interactions between Ring Theory and Representations of Algebras. Lecture Notes in Pure and Applied Mathematics 210, Marcel Dekker, Inc. (New York), 2000; 449 pp. ISBN 0 8247 0367 7 (paperack), £125 (approx.). - R. H. Villarreal. Monomial Algebras. Monographs and Textbooks in Pure and Applied Mathematics 238, Marcel Dekker, Inc. (New York), 2001; 455 pp. ISBN 0 8247 0524 6 (hardback), £126.62. - R. Wilson and J. gray. Mathematical Conversations: Selections from The Mathematical Intelligencer. Springer (Berlin), 2001; 488 pp. ISBN 0 387 98686 3 (hardback), £41.
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 305-316
- Print publication:
- December 2001
-
- Article
- Export citation
About the centroid blody and the ellipsoid of inertia
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-13
- Print publication:
- December 2001
-
- Article
- Export citation
MTK volume 48 issue 1-2 Cover and Front matter
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
Gaussian primes in narrow sectors
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 119-135
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
Finite edge-to-edge tilings by convex polygons
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-50
- Print publication:
- December 2001
-
- Article
- Export citation
Irrational dilations of Pascal's triangle
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 159-168
- Print publication:
- December 2001
-
- Article
- Export citation
Orders in completely regular semigroups
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 213-230
- Print publication:
- December 2001
-
- Article
- Export citation
Total scalar curvature and rigidity of minimal hypersurfaces in Euclidean space
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 247-251
- Print publication:
- December 2001
-
- Article
- Export citation
Geometry of the gauss map and lattice points in convex domains
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 107-117
- Print publication:
- December 2001
-
- Article
- Export citation
On sigma-phi numbers
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 169-189
- Print publication:
- December 2001
-
- Article
- Export citation
On simultaneous diagonal inequalities, II
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 191-202
- Print publication:
- December 2001
-
- Article
- Export citation
Continuous and discrete boundary value problems on the infinite interval: existence theory
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 273-292
- Print publication:
- December 2001
-
- Article
- Export citation
Difference polynomials and their generalizations
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 293-299
- Print publication:
- December 2001
-
- Article
- Export citation
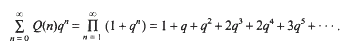
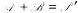 where, ℝ′ differs from the set of primes in finitely many elements only and
where, ℝ′ differs from the set of primes in finitely many elements only and 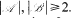 .
.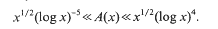
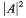 is a
is a