Refine search
Actions for selected content:
9016 results in Discrete Mathematics, Information Theory and Coding
Approximate Counting
-
-
- Book:
- Surveys in Combinatorics, 1997
- Published online:
- 29 March 2010
- Print publication:
- 31 July 1997, pp 287-324
-
- Chapter
- Export citation
Computer Construction of Block Designs
-
-
- Book:
- Surveys in Combinatorics, 1997
- Published online:
- 29 March 2010
- Print publication:
- 31 July 1997, pp 49-64
-
- Chapter
- Export citation
The Harmonious Chromatic Number and the Achromatic Number
-
-
- Book:
- Surveys in Combinatorics, 1997
- Published online:
- 29 March 2010
- Print publication:
- 31 July 1997, pp 13-48
-
- Chapter
- Export citation
Tree Width and Tangles: A New Connectivity Measure and Some Applications
-
-
- Book:
- Surveys in Combinatorics, 1997
- Published online:
- 29 March 2010
- Print publication:
- 31 July 1997, pp 87-162
-
- Chapter
- Export citation
Minor-monotone Graph Invariants
-
-
- Book:
- Surveys in Combinatorics, 1997
- Published online:
- 29 March 2010
- Print publication:
- 31 July 1997, pp 163-196
-
- Chapter
- Export citation
Some Applications of Algebraic Curves in Finite Geometry and Combinatorics
-
-
- Book:
- Surveys in Combinatorics, 1997
- Published online:
- 29 March 2010
- Print publication:
- 31 July 1997, pp 197-236
-
- Chapter
- Export citation
New Perspectives on Interval Orders and Interval Graphs
-
-
- Book:
- Surveys in Combinatorics, 1997
- Published online:
- 29 March 2010
- Print publication:
- 31 July 1997, pp 237-286
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Surveys in Combinatorics, 1997
- Published online:
- 29 March 2010
- Print publication:
- 31 July 1997, pp i-iv
-
- Chapter
- Export citation
Contents
-
- Book:
- Surveys in Combinatorics, 1997
- Published online:
- 29 March 2010
- Print publication:
- 31 July 1997, pp v-viii
-
- Chapter
- Export citation
Author Index
-
- Book:
- Surveys in Combinatorics, 1997
- Published online:
- 29 March 2010
- Print publication:
- 31 July 1997, pp 325-330
-
- Chapter
- Export citation
Finite Quasiprimitive Graphs
-
-
- Book:
- Surveys in Combinatorics, 1997
- Published online:
- 29 March 2010
- Print publication:
- 31 July 1997, pp 65-86
-
- Chapter
- Export citation
Maximum Statistics of N Random Variables Distributed by the Negative Binomial Distribution
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 June 1997, pp. 179-183
-
- Article
- Export citation
The form of the spectral functions associated with Sturm-Liouville problems with continuous spectrum
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 149-161
- Print publication:
- June 1997
-
- Article
- Export citation
A Steiner type formula for convex functions
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 195-214
- Print publication:
- June 1997
-
- Article
- Export citation
HB-subspaces and Godun sets of subspaces in Banach spaces
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 120-132
- Print publication:
- June 1997
-
- Article
- Export citation
On the Edge-Expansion of Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 June 1997, pp. 145-152
-
- Article
- Export citation
On a Theorem of Ganter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 June 1997, pp. 247-254
-
- Article
- Export citation
On a generalization of Eisenstein's irreducibility criterion
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 37-41
- Print publication:
- June 1997
-
- Article
- Export citation
Triangulations of cyclic polytopes and higher Bruhat orders
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 162-194
- Print publication:
- June 1997
-
- Article
- Export citation
Markov Processes Involving q-Stirling Numbers
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 June 1997, pp. 165-178
-
- Article
- Export citation
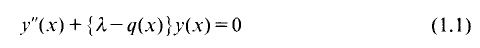
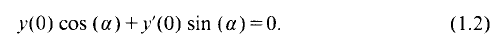
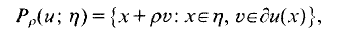
 (
( (
(