Let M be a compact flat Riemannian manifold of dimension n, and Γ its fundamental group. Then we have the following exact sequence (see [1])

where Zn is a maximal abelian subgroup of Γ and G is a finite group isomorphic to the holonomy group of M. We shall call Γ a Bieberbach group. Let T be a flat torus, and let Ggr act via isometries on T; then ┌ acts isometrically on × T where is the universal covering of M and yields a flat Riemannian structure on ( × T)/Γ. A flat-toral extension (see [9, p. 371]) of the Riemannian manifold M is any Riemannian manifold isometric to ( × T)/Γ where T is a flat torus on which Γ acts via isometries. It is convenient to adopt the convention that a single point is a 0-dimensional flat torus. If this is done, M is itself among the flat toral extensions of M. Roughly speaking, this is a way of putting together a compact flat manifold and a flat torus to make a new flat manifold the dimension of which is the sum of the dimensions of its constituents. It is, more precisely, a fibre bundle over the flat manifold with a flat torus as fibre.

In generalisation of the beta law obtained under the GEM/Poisson–Dirichlet distribution in Hirth [12] we undertake here an analogous construction which results in the Dirichlet law. Our proof makes use of Hoppe's Pólya-like urn model in population genetics.

In what follows, R will denote a commutative domain with 1, and Q(≠R) its field of quotients, which is viewed here as an R-module. By RP we denote the localization of R at the maximal ideal P, and more generally, by MP = Rp⊗RM the localization of the R-module M at P, which we define to be the P-component of M. The symbol R* will mean the multiplicative monoid of nonzero elements of R. For a submonoid S of R*, Rs will denote the localization of R at S.

It is proved that the smallest cardinality among the maximal irredundant sets in an n–vertex graph with maximum degree Δ([ges ]2) is at least 2n/3Δ. This substantially improves a bound by Bollobás and Cockayne [1]. The class of graphs which attain this bound is characterised.

An intersecting system of type (∃, ∀, k, n) is a collection []={[Fscr]1, ...,[Fscr]m} of pairwise disjoint families of k-subsets of an n-element set satisfying the following condition. For every ordered pair [Fscr]i and [Fscr]j of distinct members of [] there exists an A∈[Fscr]i that intersects every B∈[Fscr]j. Let In(∃, ∀, k) denote the maximum possible cardinality of an intersecting system of type (∃, ∀, k, n). Ahlswede, Cai and Zhang conjectured that for every k≥1, there exists an n0(k) so that In(∃, ∀, k)=(n−1/k−1) for all n>n0(k). Here we show that this is true for k≤3, but false for all k≥8. We also prove some related results.

Call a set of natural numbers subset-sum-distinct (or SSD) if all pairwise distinct subsets have unequal sums. One wants to construct SSD sets in which the largest element is as small as possible. Given any SSD set, it is easy to construct an SSD set with one more element in which the biggest element is exactly double the biggest element in the original set. For any SSD set, we construct another SSD set with k more elements whose largest element is less than 2k times the largest element in the original set. This claim has been made previously for a different construction, but we show that that claim is false.

Decompositions of simply connected 4-manifolds into three closed 4-balls are studied from the view-point of abstract regular polytopes of Schläfli type {p, q, 2, 3}. The three balls correspond to three ditopes, their common intersection corresponds to a regular map of type {p, q} as an equilibrium surface whose genus equals the “genus” of the 4-manifold.

A sharper form of the Szarek–Talagrand ‘isomorphic’ version of the Sauer–Shelah lemma is proved. Also we prove an analogous ‘isomorphic’ version of the Karpovsky–Milman lemma, which is a generalization of that due to Sauer and Shelah.

It has been known for several years that the lattice of subspaces of a finite vector space has a decomposition into symmetric chains, i.e. a decomposition into disjoint chains that are symmetric with respect to the rank function of the lattice. This paper gives a positive answer to the long-standing open problem of providing an explicit construction of such a symmetric chain decomposition for a given lattice of subspaces of a finite (dimensional) vector space. The construction is done inductively using Schubert normal forms and results in a bracketing algorithm similar to the well-known algorithm for Boolean lattices.

This paper is concerned with the analysis of locally time-synchronized slot systems for broadcast in packet radio networks. Local synchronization has been proposed in practice as less expensive than global synchronization over very wide areas, or over mobile networks. In the case of two locally coordinated groups of stations, under the assumption that the phase shift on the clocks between the two groups is random, it is shown that the probability of no collision is maximized when occupied slots within each group are chosen consecutively, regardless of the number of total slots, or the number of occupied slots in either group.

In this note we point out that a simple proof of the lower bound of the sets (b, c), and so also of Ξ(b, c), defined in the previous paper [1] can be obtained as a simple application of a general method. By Example 4.6 from [2], if [0, 1] = E0⊃E1⊃ … are sets each of which is a finite union of disjoint closed intervals such that each interval of Ek−1, contains at least mk intervals of Ek which are separated by gaps of lengths at least εk, and if mk≥2 and εk≥εk+1>0, then the dimension of the intersection of Ek is at least

We introduce a class of “differential operators” on graphs and we prove an energy estimate and a Liouville type theorem depending on some structural properties of the operators considered.

We explore the ‘Hausdorff dimension at infinity’ for self-affine carpets defined on the square lattice. This notion of dimension (due to Barlow and Taylor), which is the correct notion from a probabilistic perspective, differs for these sets from more ‘naive’ indices of fractal dimension.

We provide a unified and simplified proof that for any partition of (0, 1] into sets that are measurable or have the property of Baire, one cell will contain an infinite sequence together with all of its sums (finite or infinite) without repetition. In fact any set which is large around 0 in the sense of measure or category will contain such a sequence. We show that sets with 0 as a density point have very rich structure. 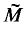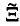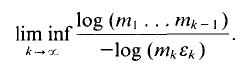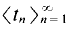Call a sequence and its resulting all-sums set 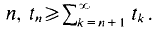structured provided for each We show further that structured all-sums sets with positive measure are not partition regular even if one allows shifted all-sums sets. That is, we produce a two cell measurable partition of (0, 1 ] such that neither set contains a translate of any structured all-sums set with positive measure.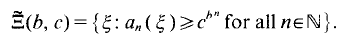

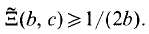A number of known estimates of the number of translates, or lattice translates, of a convex body H required to cover a convex body K are obtained as consequences of two simple results.

Let [0;a1(ξ), a2(ξ),…] denote the continued fraction expansion of ξ∈[0, 1]. The problem of estimating the fractional dimension of sets of continued fractions emerged in late twenties in papers by Jarnik [6, 7] and Besicovitch [1] and since then has been addressed by a number of authors (see [2, 4, 5, 8, 9]). In particular, Good [4] proved that the set of all ξ, for which an(ξ)→∞ as n→∞ has the Hausdorff dimension ½ For the set of continued fractions whose expansion terms tend to infinity doubly exponentially the dimension decreases even further. More precisely, let

Hirst [5] showed that dim On the other hand, Moorthy [8] showed that dim 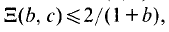where

In this paper we investigate the solutions in integers x, y, z, X, Y, Z of the system

where P is a real number that may be taken to be arbitrarily large, and the (fixed) integer exponent h satisfies h≥4. The system has 6P3 + O(P2) “trivial” solutions in which x, y, z are a permutation of X, Y, Z. Our result implies that the number of non-trivial solutions is at most o(P3), so that the total number of solutions is asymptotic to 6P3.

Let (Sn)n = 1,2,… be the strictly increasing sequence of those natural numbers that can be represented as the sum of three cubes of positive integers. The estimate

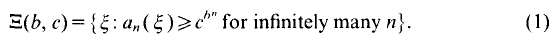
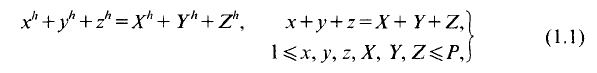
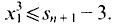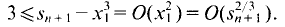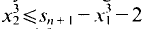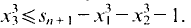is easily proved as follows: Let x1 be the largest natural number with Then This procedure is iterated by choosing x2 and then x3 as the largest natural numbers satisfying and Thus 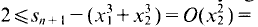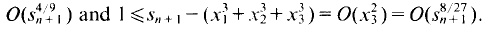Since 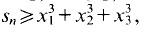this implies (1).

Recently, it has been shown that tight or almost tight upper bounds for the discrepancy of many geometrically denned set systems can be derived from simple combinatorial parameters of these set systems. Namely, if the primal shatter function of a set system ℛ on an n-point set X is bounded by const. md, then the discrepancy disc (ℛ) = O(n(d−1)/2d) (which is known to be tight), and if the dual shatter function is bounded by const. 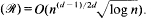md, then disc We prove that for d = 2, 3, the latter bound also cannot be improved in general. We also show that bounds on the shatter functions alone do not imply the average (L1)-discrepancy to be much smaller than the maximum discrepancy: this contrasts results of Beck and Chen for certain geometric cases. In the proof we give a construction of a certain asymptotically extremal bipartite graph, which may be of independent interest.