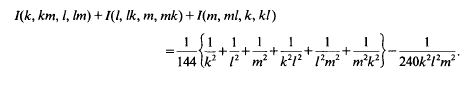Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
Ascendant subgroups of factorized FC-groups
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 188-189
- Print publication:
- June 1995
-
- Article
- Export citation
Some examples of groups with no non-trivial action on a Λ-tree
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 214-219
- Print publication:
- June 1995
-
- Article
- Export citation
Symbolic powers and local cohomology
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 182-187
- Print publication:
- June 1995
-
- Article
- Export citation
On metrizable E with Cp(E) ≇ Cp(E) × Cp(E)
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-55
- Print publication:
- June 1995
-
- Article
- Export citation
How do convex bodies sit?
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 178-181
- Print publication:
- June 1995
-
- Article
- Export citation
A sharp inequality of Halász type for the mean value of a multiplicative arithmetic function
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 144-157
- Print publication:
- June 1995
-
- Article
- Export citation
Unions of products of independent sets
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-29
- Print publication:
- June 1995
-
- Article
- Export citation
Representation extensions and amalgamation bases in rings
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 394-400
- Print publication:
- December 1994
-
- Article
- Export citation
MTK volume 41 issue 2 Cover and Front matter
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
Boundedness for a system of reaction-diffusion equations 1
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 293-300
- Print publication:
- December 1994
-
- Article
- Export citation
Solvability of semilinear abstract equations at resonance
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 301-311
- Print publication:
- December 1994
-
- Article
- Export citation
Book Reviews - N. Bourbaki. Elements of the History of Mathematics. Springer. 1994, 301 pp., DM 78. - A. Dolan and J. Aldous Networks and Algorithms. An Introductory Approach. J. Wiley. 1993, 544 pp., £19·95. - A. J. Feingold, I. B. Frenkel and J. F. X. Ries Spinor construction of vertex operator algebras, triality and E8(1). American Mathematical Society. 1991, 146 pp., £23. - N. D. Fowkes and J. J. Mahony. An Introduction to Mathematical Modelling. J. Wiley. 1994, 447 pp., £19·95 - J. R. Garratt. The Atmospheric Boundary LayerCambridge University Press. 1994, 316 pp., £19·95. - O. Gingerich. The eye of heaven: Ptolemy, Copernicus, Kepler. American Institute of Physics. 1993, 442 pp., £24·50. - N. V. Govorov. Riemann's boundary problem with infinite index. Birkhauser. 1994, 248 pp., Swiss Fr. 148 - I. O. Grattan-Guinness, Editor. Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences. Routledge. 1994, 2 vols, 1806 pp.in all, £140. - U. Grenander General Pattern Theory. Clarendon Press, Oxford. 1993, 883 pp, £130. - O. L. R. Jacobs. Introduction to Control Theory. Oxford University Press. 1993, 390 pp., £22·50. - V. J. Katz. A History of Mathematics: an introduction. Harper-Collins. 1993, 786 pp., £19·99. - W. R. Knorr. The Ancient Tradition of Geometric Problems. Dover. 1993, 410 pp., Paper-back $12.95. - R. Lidl and H. Niederreiter Introduction to Finite Fields and their Applications. Revised Edition. Cambridge University Press. 1994, 416 pp., £29·95. - Y. V. Matiyasevich. Hilbert's Tenth Problem. MIT Press. 1993, 264 pp., £40·50. - A. I. Miller. Early Quantum Electrodynamics: A Source Book. Cambridge University Press. 1994, 265 pp., £40. - P. M. Neumann, G. A. Stoy and E. C. Thompson. Groups and Geometry. Oxford University Press. 1994, 254 pp., £19·50. - T. W. Palmer. Banach Algebras and the General Theory of *-algebras. Vol. 1. Algebras and Banach Algebras. Vol. 49 of the Encyclopedia of Mathematics and its Application. Cambridge University Press. 1994, 794 pp., £60. - W. F. Pfeffer. The Riemann approach to integration: local geometric theory. Cambridge University Press. 1994, 302 pp., £30. - D. Salamon, Editor. Symplectic Geometry, L.M.S. Lecture Notes no 192. Cambridge University Press. 1994, 236 pp., £25. - D. W. L. Sumners, Editor. New Scientific Applications of Geometry and Topology. Proceedings of Symposia in Applied Mathematics. Vol 45. American Mathematical Society. 1992, 250 pp., $49. - W. V. Vasconcelos. Arithmetic of Blowup Algebras. L.M.S. Lecture Notes Series, no 195. Cambridge University Press. 1994, 329 pp., £22·95. - T. J. Willmore. Riemannian Geometry. Clarendon Press, Oxford. 1993, 318 pp., £45.
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 402-406
- Print publication:
- December 1994
-
- Article
- Export citation
Coxeter-associahedra
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 364-393
- Print publication:
- December 1994
-
- Article
- Export citation
Disjoint embeddings of compacta
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 221-232
- Print publication:
- December 1994
-
- Article
- Export citation
On uniformly Gâteaux differentiable norms in C(K)
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 233-238
- Print publication:
- December 1994
-
- Article
- Export citation
The asymptotic formula in Waring's problem
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 329-347
- Print publication:
- December 1994
-
- Article
- Export citation
Characterizations of the critical Stokes number for potential and viscous flows
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 277-292
- Print publication:
- December 1994
-
- Article
- Export citation
Comparison theorems of Sturm's type
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 312-321
- Print publication:
- December 1994
-
- Article
- Export citation
Random Banach spaces: The limitations of the method
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 239-250
- Print publication:
- December 1994
-
- Article
- Export citation
Multiple Franel integrals: Corrigendum
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, p. 401
- Print publication:
- December 1994
-
- Article
- Export citation
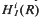 , and the comparison of the topologies defined by the
, and the comparison of the topologies defined by the 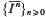
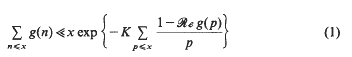
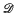 for all primes
for all primes 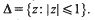 Thus our point of view is similar to that of Halász [Hz 2] in that we seek a general inequality in terms of simple quantities, albeit
Thus our point of view is similar to that of Halász [Hz 2] in that we seek a general inequality in terms of simple quantities, albeit 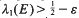 and
and 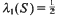 and
and 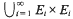 where the sets
where the sets 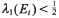 . The results of this paper answer questions of M. Laczkovich and are related to a paper of D. H. Fremlin.
. The results of this paper answer questions of M. Laczkovich and are related to a paper of D. H. Fremlin.
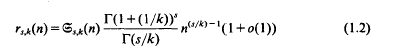
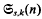 , the
, the 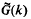 to be the smallest value of
to be the smallest value of 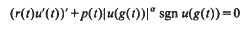
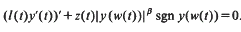
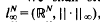 , or equivalently, -typical
, or equivalently, -typical 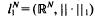 , where the meaning of what is typical and what is not is defined in terms of the Haar measure
, where the meaning of what is typical and what is not is defined in terms of the Haar measure 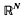 .
.