Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
On the positivity of solutions to the Smoluchowski equations
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 406-412
- Print publication:
- December 1995
-
- Article
- Export citation
A second genus of regular ternary forms
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 444-447
- Print publication:
- December 1995
-
- Article
- Export citation
Reconstructing curves from sets of quantized observations
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 340-353
- Print publication:
- December 1995
-
- Article
- Export citation
A short proof of Hadwiger's characterization theorem
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 329-339
- Print publication:
- December 1995
-
- Article
- Export citation
Radiation of acoustic power from a two-dimensional double elastic panel
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 368-391
- Print publication:
- December 1995
-
- Article
- Export citation
Low dimensional lattices have a strict Voronoï basis
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 229-238
- Print publication:
- December 1995
-
- Article
- Export citation
Coefficient multipliers between Bergman and Hardy spaces
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 413-426
- Print publication:
- December 1995
-
- Article
- Export citation
Thin non-lattice covering with an affine image of a strictly convex body
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 239-250
- Print publication:
- December 1995
-
- Article
- Export citation
Intersection bodies and ellipsoids
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 295-304
- Print publication:
- December 1995
-
- Article
- Export citation
Cubic Diophantine inequalities
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 264-277
- Print publication:
- December 1995
-
- Article
- Export citation
Book Reviews - N. Biggs. Algebraic Graph Theory. 2nd Edition. Cambridge University Press. 1993, ISBN 0 521 45897 8, 205 pp., paperback, £14.95. - S. Chandrasekhar. Newton's Principia for the Common Reader. Clarendon Press. 1995, ISBN 0 198 51744 0, 595 pp., £75. - V. Chari and A. Pressley. A Guide to Quantum Groups. Cambridge University Press. 1995, ISBN 0 521 55884 0, 651 pp., paperback, £22.95. - I. B. Cohen and R. S. Westfall, Editors. Newton: texts, backgrounds, commentaries. Norton. 1995, ISBN 0 393 95902 3, 434 pp., paperback, £6.95. - R. W. R. Darling. Differential Forms and Connections. Cambridge University Press. 1994, ISBN 0 521 46800 0, 256 pp., paperback, £12.95. - J. W. Dauben. Abraham Robinson, the Creation of Nonstandard Analysis, a Personal and Mathematical Odyssey. Princeton University Press. 1995, ISBN 0 691 03745 0, 559 pp., £40. - H. M. Edwards. Linear Algebra. Birkhäuser. 1995, ISBN 3 7643 3731 1, 184 pp., DM68. - P. Glendinning. Stability, Instability and Chaos. Cambridge University Press. 1994, ISBN 0 521 42566 2, 388 pp., paperback, £17.95. - C. D. Godsil. Algebraic Combinatorics. Chapman and Hall. 1993, ISBN 0 412 041316, 362 pp., £45. - C. Hakfoort. Optics in the age of Euler, conceptions of the nature of light, 1700-1795. Cambridge University Press. 1995, ISBN 0 52140471 1, 243 pp., £35. - D. Hilbert. Theory of Algebraic Invariants. Cambridge University Press. 1993, ISBN 0 521 44903 0, 191 pp., paperback, £12.95. - S. Kaufmann. Mathematica as a tool. Birkhäuser. 1994, ISBN 3 7643 5031 8, 448 pp., £24.40. - A. Lubotzky. Discrete Groups, Expanding Graphs and Invariant Measures. Birkhäuser. 1994, ISBN 3 7643 5075 X, 195 pp., £35. - F. S. Macaulay. The Algebraic Theory of Modular Systems. Cambridge University Press. 1994, ISBN 0 521 45562 6, 112 pp., paperback, £12.95. - M. S. Mahoney. The mathematical career of Pierre de Fermat, 1601–1665. 2nd Edition. Princeton University Press. 1994, ISBN 0 691 03666 7, 432 pp., £16.25. - P. Mattila. Geometry of Sets and Measures in Euclidean Spaces. Fractals and rectifiability. Cambridge University Press. 1995, ISBN 0 521 46576 1, 344 pp., £35. - S. Montgomery. Hopf algebras and their actions on rings. American Mathematical Society. 1993, ISBN 0 8218 0738 2, 238 pp., paperback, £28. - P. I. Naumkin and I. A. Shishmarev. Nonlinear nonlocal Equations in the Theory of Waves. American Mathematical Society. 1994, ISBN 0 8218 4573 X, 289 pp., $149. - R. J. Plymen and P. L. Robinson. Spinors in Hilbert space. Cambridge Tracts in Mathematics, 114. Cambridge University Press. 1994, ISBN 0 521 45022 5, 165 pp., £25. - V. V. Prasolov. Intuitive Topology. American Mathematical Society. 1995, ISBN 0 8218 0356 5, 95 pp., £25.00. - L. C. G. Rogers and D. Williams. Diffusions, Markov Processes and Martingales. Volume 1: Foundations. 2nd Edition. Wiley. 1994, ISBN 0 471950610, 386 pp., £49.95. - L. Schneps, Editor. The Grothendieck Theory of Dessins d'Enfants. LMS Lecture Notes Series, 200. Cambridge University Press. 1994, ISBN 0 521 47821 9, 368 pp., £24.95. - M. Senechal. Quasicrystals and Geometry. Cambridge University Press. 1995, ISBN 0 521 37259 3, 286 pp., £40. - A. M. Sinclair and R. R. Smith. Hochschild cohomology of von Neumann Algebras. LMS Lecture Notes, 203. Cambridge University Press. 1995, ISBN 0 521 47880 4, 196 pp., paperback, £19.95. - K. Spindler. Abstract Algebra with Applications, Vols I and II. Dekker. 1994, ISBN 0 8247 9144 4 and 0 8247 9159 2, 531pp. and 756 pp., $75 per volume or $125 for both. - G. Tenenbaum. Introduction to analytic and probabilistic number theory. Cambridge University Press. 1995, ISBN 0 521 41261 7, 448 pp., £45.
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 448-453
- Print publication:
- December 1995
-
- Article
- Export citation
Index to volume 42
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 455-456
- Print publication:
- December 1995
-
- Article
- Export citation
Regularity and products of idempotents in endomorphism monoids of projective acts
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 354-367
- Print publication:
- December 1995
-
- Article
- Export citation
2 - L-matrices
-
- Book:
- Matrices of Sign-Solvable Linear Systems
- Published online:
- 04 February 2010
- Print publication:
- 29 September 1995, pp 18-34
-
- Chapter
- Export citation
1 - Sign-solvability
-
- Book:
- Matrices of Sign-Solvable Linear Systems
- Published online:
- 04 February 2010
- Print publication:
- 29 September 1995, pp 1-17
-
- Chapter
- Export citation
Preface
-
- Book:
- Matrices of Sign-Solvable Linear Systems
- Published online:
- 04 February 2010
- Print publication:
- 29 September 1995, pp xi-xii
-
- Chapter
- Export citation
5 - Beyond S* -matrices
-
- Book:
- Matrices of Sign-Solvable Linear Systems
- Published online:
- 04 February 2010
- Print publication:
- 29 September 1995, pp 87-105
-
- Chapter
- Export citation
9 - The inverse sign pattern graph
-
- Book:
- Matrices of Sign-Solvable Linear Systems
- Published online:
- 04 February 2010
- Print publication:
- 29 September 1995, pp 225-238
-
- Chapter
- Export citation
8 - Extremal properties of L-matrices
-
- Book:
- Matrices of Sign-Solvable Linear Systems
- Published online:
- 04 February 2010
- Print publication:
- 29 September 1995, pp 203-224
-
- Chapter
- Export citation
Index
-
- Book:
- Matrices of Sign-Solvable Linear Systems
- Published online:
- 04 February 2010
- Print publication:
- 29 September 1995, pp 295-298
-
- Chapter
- Export citation
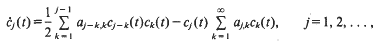

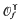 of
of 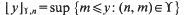
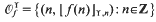
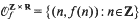 and
and 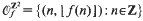 , where [x] (without subscript) denotes as usual the integer part of
, where [x] (without subscript) denotes as usual the integer part of 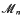 . This is then used to prove that a Minkowski reduced basis of a lattice of dimension
. This is then used to prove that a Minkowski reduced basis of a lattice of dimension 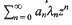 belongs to
belongs to 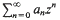 belongs to
belongs to 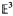 with certain congruent ellipsoids.
with certain congruent ellipsoids.