Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
Lattice packing of spheres and the Wulff-Shape
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 229-236
- Print publication:
- December 1996
-
- Article
- Export citation
Index to Volume 43
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 428-429
- Print publication:
- December 1996
-
- Article
- Export citation
Existence and uniqueness for a class of mixed type differential equations
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 382-392
- Print publication:
- December 1996
-
- Article
- Export citation
H.J. Baues. Homotopy Type and Homology. Clarendon Press. 1996, ISBN 0 19 851482 4, 483pp., £80. - J. B. Brackenridge. The Key to Newton's Dynamics: the Kepler Problem and the Principia. University of California Press. 1995, ISBN 0 520 20217 1, 299pp., paperback £15.95. - H. Clemens and J. Kollár. Editors. Current Topics in Complex Algebraic Geometry. Cambridge University Press. 1995, ISBN 0 52156244 9, 158pp., hardback £24. - J. Cofman. Numbers and Shapes Revisited: More Problems for Young Mathematicians. Clarendon Press. 1995, ISBN 0 19 853460 4, 308pp., £19·50. - F. de Gandt. Force and Geometry in Newton's Principia. Princeton University Press. 1995, ISBN 0 691 03367 6, 297pp., £35. - C. R. Doering and J. D. Gibbon. Applied analysis of the Navier-Stokes equations. Cambridge University Press. 1995, ISBN 0 521 44557 4, 217pp., hardback £40. - N. D. Gilbert and T. Porter. Knots and Surfaces. Oxford University Press. 1995, ISBN 0 19 851490 5, 268pp., paperback £19·50. - J. L. Greenberg. The Problem of the Earth's Shape from Newton to Clairaut: the Rise of Mathematical Science in Eighteenth Century Paris and the Fall of “Normal” Science. Cambridge University Press. 1995, ISBN 0 521 38541 5, 781pp., £60. - M. Holschneider. Wavelets: An Analysis Tool. Clarendon Press. 1995, ISBN 0 19 853481 7, 423pp., £45. - J. Kollár. Rational Curves on Algebraic Varieties. Ergebn. d. Math. (3) 32. Springer. 1996, ISBN 3 540 60168 6, 320pp., DM158. - G. Laumon. Cohomology of Drinfeld Modular Varieties. Part I: Geometry, counting of points and local harmonic analysis. Cambridge University Press. 1996, ISBN 0 521 47060 9, 344pp., £40. - A. Pfister. Quadratic Forms with Applications to Algebraic Geometry and Topology. Cambridge University Press. 1995, ISBN 0 52146755 1, 179pp., paperback £22.95 - I. A. Porteous. Clifford Algebras and the Classical Groups. Cambridge University Press. 1995, ISBN 0 521 55177 3, 295pp., £30. - M. Reid. Undergraduate Commutative Algebra. LMS Student Text 29. Cambridge University Press. 1995, ISBN 0 521 45889 7, 153pp., paperback £11·95. - J. Ryan. Clifford Algebras in Analysis and Related Topics. CRC Press Boca Raton. 1996, ISBN 0 8493 8481 8, 366pp., in U.S. $79.95, outside U.S. $96.00. - L. R. Vermani. Elements of Algebraic Coding Theory. Chapman and Hall. 1996, ISBN 0 412 57380 6, 254pp., paperback £27·50 - A. I. Zayed. Handbook of Function and Generalized Function Transformations. CRC Press Boca Raton. 1996, ISBN 0 8493 7851 6, 643pp., $69.95
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 424-427
- Print publication:
- December 1996
-
- Article
- Export citation
A pair correlation hypothesis and the exceptional set in Goldbach's problem
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 349-361
- Print publication:
- December 1996
-
- Article
- Export citation
Volumes of projection bodies
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 255-264
- Print publication:
- December 1996
-
- Article
- Export citation
The effect of surface tension on the scattering of waves by a partially immersed vertical barrier in water of infinite depth
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 182-197
- Print publication:
- June 1996
-
- Article
- Export citation
Simple valuations on convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 32-39
- Print publication:
- June 1996
-
- Article
- Export citation
Barycentric subdivision of triangles and semigroups of Möbius maps
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 165-171
- Print publication:
- June 1996
-
- Article
- Export citation
σ-fragmentability and analyticity
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 172-181
- Print publication:
- June 1996
-
- Article
- Export citation
Order-two density and the strong law of large numbers
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-22
- Print publication:
- June 1996
-
- Article
- Export citation
The asymptotic form of the Titchmarsh-weyl m-function associated with a non-definite, linear, second order differential equation
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 209-222
- Print publication:
- June 1996
-
- Article
- Export citation
Explicit bounds on exponential sums and the scarcity of squarefree binomial coefficients
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 73-107
- Print publication:
- June 1996
-
- Article
- Export citation
On a question of regarding visibility of lattice points
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 155-158
- Print publication:
- June 1996
-
- Article
- Export citation
Asymptotic theory for a class of fourth-order differential equations
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 198-208
- Print publication:
- June 1996
-
- Article
- Export citation
Estimates of hybrid exponential sums on quasiprojective varieties over finite fields
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-72
- Print publication:
- June 1996
-
- Article
- Export citation
Epsilon entropy and the packing of balls in Euclidean space
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 23-31
- Print publication:
- June 1996
-
- Article
- Export citation
Bounds on the covering radius of a lattice
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 159-164
- Print publication:
- June 1996
-
- Article
- Export citation
Irregularities of distributions with respect to polytopes
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 108-119
- Print publication:
- June 1996
-
- Article
- Export citation
MTK volume 43 issue 1 Cover and Front matter
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
- Print publication:
- June 1996
-
- Article
-
- You have access
- Export citation
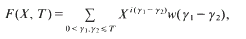
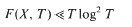
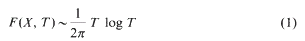
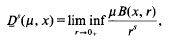
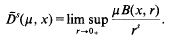

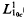 (0, ∞) and λ is a complex number with
(0, ∞) and λ is a complex number with
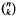 must be highly composite in that it contains many prime factors and often to high powers. It is therefore of interest to enquire as to how infrequently
must be highly composite in that it contains many prime factors and often to high powers. It is therefore of interest to enquire as to how infrequently 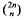 is not squarefree once
is not squarefree once 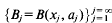 be a sequence of mutually disjoint open balls, with centres
be a sequence of mutually disjoint open balls, with centres 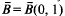 in
in 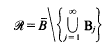
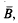 the balls {
the balls {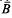 provided that λ(ℛ)=0, where λ denotes the
provided that λ(ℛ)=0, where λ denotes the 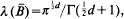 henceforth denoted by
henceforth denoted by 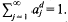 Larman [11] has noted that, under these circumstances, one also has
Larman [11] has noted that, under these circumstances, one also has 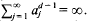 .
.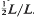 . The convex hull of all minimal vectors of a class
. The convex hull of all minimal vectors of a class 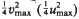 be a maximal squared radius of
be a maximal squared radius of 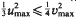 , then
, then 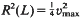 . This is the case in the well-known Barnes-Wall and Leech lattices. Otherwise,
. This is the case in the well-known Barnes-Wall and Leech lattices. Otherwise, 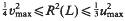 . This is a refinement of a result of Norton ([3], Ch. 22).
. This is a refinement of a result of Norton ([3], Ch. 22).