Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
Relative norms of prime ideals in small regions
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 40-62
- Print publication:
- June 1996
-
- Article
- Export citation
The higher Stasheff-Tamari posets
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-154
- Print publication:
- June 1996
-
- Article
- Export citation
On the number of cells defined by a family of polynomials on a variety
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 120-126
- Print publication:
- June 1996
-
- Article
- Export citation
J. L. Alperin and R. B. Bell. Groups and Representations. Springer.1995, ISBN 0 387 94526 1, 194 pp., Softcover, DM 38. - W. S. Anglin and J. Lambek. The Heritage of Thales. Springer. 1995, ISBN 0 387 94544 X, 327 pp., DM 58. - A. V. Arhangel'skii. Editor. General Topology II. Encyclopaedia of Mathematical Sciences, Vol. 50. Springer. 1995, ISBN 3 540 54695 2, 256 pp., DM 148. - V. I. Arnautov, S. T. Glavatsky and A. V. Mikhalev. Introduction to the Theory of Topological Rings and Modules. Marcel Dekker. 1995, ISBN 0 8247 9323 4, 502 pp., $165. - H. F. Baker. Abelian Functions: Abel's Theorem and the Allied Theory of Theta Functions. New edition, first published in 1897. Cambridge University Press. 1995, ISBN 0 521 49877 5, 684 pp., £27·95. - K. I. Beider, W. S. MartindaleIII and A. V. Mikhalev. Rings with Generalized Identities. Marcel Dekker. 1996, ISBN 0 8247 9325 0, 517 pp., $185. - R. A. Brualdi and B. L. Shader. Matrices of Sign-Solvable Systems. Cambridge Tracts in Mathematics. Cambridge University Press. 1995, ISBN 0 521 48296 8, 298 pp., £30. - H. Cohen. A Course in Computational Algebraic Number Theory. Springer Graduate Texts in Mathematics. Second corrected printing. Springer. 1995, ISBN 3 540 55640 0, 534 pp., £34.50. - P. M. Cohn. Skew Fields. Encyclopaedia of Mathematics and its Applications, Vol. 57. Cambridge University Press. 1995, ISBN 0 521 43217 0, 500 pp., £55. - S. C. Coutinho. A Primer of Algebraic D-modules. LMS Student Texts, 33. Cambridge University Press. 1995, ISBN 0 521 55119 6, 207 pp., £30.00. - P. J. Davis, R. Hersh and E. A. Marchisotto. The Mathematical Experience. Study Edition. Birkhauser. 1995, ISBN 0 8176 3739 7, 487 pp., DM 78. - R. J. Gardner. Geometric Tomography. Cambridge University Press. 1995, ISBN 0 521 45126 4, 424 pp., £45. - I. M. Gelfand, M. M. Kapranov and A. V. Zelevinsky. Discriminants, Resultants and Multidimensional Determinants. Birkhauser. 1994, ISBN 3 7643 3660 9, 523 pp., DM 158. - A. Katok and B. Hasselblatt. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press. 1995, ISBN 0 521 34187 6, 802 pp., £60. - J. Krajícek. Bounded Arithmetic, Propositional Logic, and Complexity Theory. Cambridge University Press. 1995, ISBN 0 521 45205 8, 343 pp., £40. - J. McCleary. Geometry from a Differentiable Viewpoint. Cambridge University Press. 1994, ISBN 0 521 42480 1, 308 pp., Paperback £14·95. - D. McDuff and D. Salamon. Introduction to Symplectic Topology. Clarendon Press. 1995, ISBN 0 19 851177 9, 425 pp., £45. - C. McLarty. Elementary Categories, Elementary Toposes. Clarendon Press. 1995, ISBN 0 19 851473 5, 265 pp., £25. - R. A. Mollin. Quadratics. CRC Press. 1996, ISBN 0 8493 3983 9, 387 pp., $74.95. - S. P. Novikov. Topology I, General Survey. Encyclopaedia of Mathematical Sciences, Vol. 12. Springer. 1996, ISBN 0 387 17007 3, 319 pp., Hardcover, DM 148. - D. J. S. Robinson. A Course in the Theory of Groups. 2nd Edition. Springer. 1996, ISBN 0 387 94461 3, 499 pp., Hardcover, DM 88. - Sasaki Chikara, Sugiura Mitsuo and J. W. Dauben. Editors. The Intersection of History and Mathematics. Birkhäuser. 1994, ISBN 0 8176 5029 6, 257 pp., £56. - I. R. Shafarevich, Editor. Algebraic Geometry II. Encyclopaedia of Mathematical Sciences, Vol. 35. Springer. 1996, ISBN 3 540 54680 4, 262 pp., Hardcover, DM 148. - J. Thévenaz. G-algebras and Modular Representation Theory. Oxford University Press. 1995, ISBN 0 19 853587 2, 570 pp., £65.
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 223-228
- Print publication:
- June 1996
-
- Article
- Export citation
Principles underlying the degeneracy of models of the untyped lambda calculus
-
-
- Book:
- Semigroup Theory and its Applications
- Published online:
- 05 April 2013
- Print publication:
- 16 May 1996, pp 123-156
-
- Chapter
- Export citation
Bands of semigroups: variations on a Clifford Theme
-
-
- Book:
- Semigroup Theory and its Applications
- Published online:
- 05 April 2013
- Print publication:
- 16 May 1996, pp 53-80
-
- Chapter
- Export citation
Reminiscences of a friendship
-
-
- Book:
- Semigroup Theory and its Applications
- Published online:
- 05 April 2013
- Print publication:
- 16 May 1996, pp 1-2
-
- Chapter
- Export citation
Maps implicit in the Jordan-Hölder theorem
-
-
- Book:
- Semigroup Theory and its Applications
- Published online:
- 05 April 2013
- Print publication:
- 16 May 1996, pp 95-106
-
- Chapter
- Export citation
I - Historical Perspective
-
- Book:
- Semigroup Theory and its Applications
- Published online:
- 05 April 2013
- Print publication:
- 16 May 1996, pp 3-4
-
- Chapter
- Export citation
Contents
-
- Book:
- Semigroup Theory and its Applications
- Published online:
- 05 April 2013
- Print publication:
- 16 May 1996, pp v-vi
-
- Chapter
- Export citation
Finite semigroups as categories, ordered semigroups or compact semigroups
-
-
- Book:
- Semigroup Theory and its Applications
- Published online:
- 05 April 2013
- Print publication:
- 16 May 1996, pp 107-122
-
- Chapter
- Export citation
Isbell's zigzag theorem and its consequences
-
-
- Book:
- Semigroup Theory and its Applications
- Published online:
- 05 April 2013
- Print publication:
- 16 May 1996, pp 81-92
-
- Chapter
- Export citation
A survey on totally ordered semigroups
-
-
- Book:
- Semigroup Theory and its Applications
- Published online:
- 05 April 2013
- Print publication:
- 16 May 1996, pp 15-40
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Semigroup Theory and its Applications
- Published online:
- 05 April 2013
- Print publication:
- 16 May 1996, pp i-iv
-
- Chapter
- Export citation
Special involutions
-
-
- Book:
- Semigroup Theory and its Applications
- Published online:
- 05 April 2013
- Print publication:
- 16 May 1996, pp 157-165
-
- Chapter
- Export citation
The relationship of Al Clifford's work to the current theory of semigroups
-
-
- Book:
- Semigroup Theory and its Applications
- Published online:
- 05 April 2013
- Print publication:
- 16 May 1996, pp 43-52
-
- Chapter
- Export citation
II - Current Trends
-
- Book:
- Semigroup Theory and its Applications
- Published online:
- 05 April 2013
- Print publication:
- 16 May 1996, pp 41-42
-
- Chapter
- Export citation
A. H. Clifford's work on unions of groups
-
-
- Book:
- Semigroup Theory and its Applications
- Published online:
- 05 April 2013
- Print publication:
- 16 May 1996, pp 5-14
-
- Chapter
- Export citation
III - New Directions
-
- Book:
- Semigroup Theory and its Applications
- Published online:
- 05 April 2013
- Print publication:
- 16 May 1996, pp 93-94
-
- Chapter
- Export citation
Foreword
-
- Book:
- Semigroup Theory and its Applications
- Published online:
- 05 April 2013
- Print publication:
- 16 May 1996, pp vii-x
-
- Chapter
- Export citation
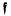 a fixed integral ideal and
a fixed integral ideal and 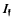 the group of fractional ideals of
the group of fractional ideals of 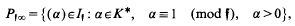
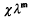 be an arbitrary Groessencharaktere mod f as defined in [15]. Then
be an arbitrary Groessencharaktere mod f as defined in [15]. Then 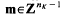 and, for
and, for 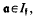
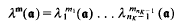
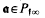 depends only on the
depends only on the 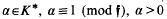 that exists such that
that exists such that 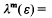 1 for all units ε in
1 for all units ε in 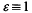 (mod
(mod 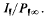
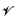 a variety of real dimension
a variety of real dimension 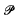 = {
= {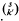 (
(