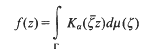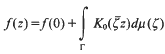Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
Introduction
-
- Book:
- Combinatorial Methods in Discrete Mathematics
- Published online:
- 22 March 2010
- Print publication:
- 11 January 1996, pp xi-xiv
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Combinatorial Methods in Discrete Mathematics
- Published online:
- 22 March 2010
- Print publication:
- 11 January 1996, pp i-iv
-
- Chapter
- Export citation
6 - Pólya's theorem and its applications
-
- Book:
- Combinatorial Methods in Discrete Mathematics
- Published online:
- 22 March 2010
- Print publication:
- 11 January 1996, pp 272-294
-
- Chapter
- Export citation
4 - Graphs and mappings
-
- Book:
- Combinatorial Methods in Discrete Mathematics
- Published online:
- 22 March 2010
- Print publication:
- 11 January 1996, pp 165-208
-
- Chapter
- Export citation
Bibliography
-
- Book:
- Combinatorial Methods in Discrete Mathematics
- Published online:
- 22 March 2010
- Print publication:
- 11 January 1996, pp 295-302
-
- Chapter
- Export citation
5 - The general combinatorial scheme
-
- Book:
- Combinatorial Methods in Discrete Mathematics
- Published online:
- 22 March 2010
- Print publication:
- 11 January 1996, pp 209-271
-
- Chapter
- Export citation
Preface to the English edition
-
- Book:
- Combinatorial Methods in Discrete Mathematics
- Published online:
- 22 March 2010
- Print publication:
- 11 January 1996, pp ix-x
-
- Chapter
- Export citation
Preface
-
- Book:
- Combinatorial Methods in Discrete Mathematics
- Published online:
- 22 March 2010
- Print publication:
- 11 January 1996, pp vii-viii
-
- Chapter
- Export citation
3 - Generating functions
-
- Book:
- Combinatorial Methods in Discrete Mathematics
- Published online:
- 22 March 2010
- Print publication:
- 11 January 1996, pp 102-164
-
- Chapter
- Export citation
Index
-
- Book:
- Combinatorial Methods in Discrete Mathematics
- Published online:
- 22 March 2010
- Print publication:
- 11 January 1996, pp 303-306
-
- Chapter
- Export citation
Contents
-
- Book:
- Combinatorial Methods in Discrete Mathematics
- Published online:
- 22 March 2010
- Print publication:
- 11 January 1996, pp v-vi
-
- Chapter
- Export citation
1 - Combinatorial configurations
-
- Book:
- Combinatorial Methods in Discrete Mathematics
- Published online:
- 22 March 2010
- Print publication:
- 11 January 1996, pp 1-48
-
- Chapter
- Export citation
2 - Transversals and permanents
-
- Book:
- Combinatorial Methods in Discrete Mathematics
- Published online:
- 22 March 2010
- Print publication:
- 11 January 1996, pp 49-101
-
- Chapter
- Export citation
Foundations of a theory of convexity on affine Grassmann manifolds
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 305-328
- Print publication:
- December 1995
-
- Article
- Export citation
A counterexample in parabolic potential theory
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 392-396
- Print publication:
- December 1995
-
- Article
- Export citation
Ramanujan's explicit values for the classical theta-function
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 278-294
- Print publication:
- December 1995
-
- Article
- Export citation
Matrix transformations of series of orthogonal polynomials
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 427-443
- Print publication:
- December 1995
-
- Article
- Export citation
A new approach to covering
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 251-263
- Print publication:
- December 1995
-
- Article
- Export citation
Multipliers of Cauchy integrals of logarithmic potentials
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 397-405
- Print publication:
- December 1995
-
- Article
- Export citation
MTK volume 42 issue 2 Cover and Front matter
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
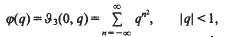
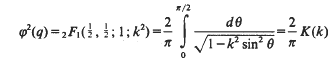
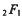 denotes the ordinary or Gaussian hypergeometric function;
denotes the ordinary or Gaussian hypergeometric function; 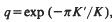
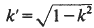 is the complementary modulus. Thus, an evaluation of any one of the functions φ,
is the complementary modulus. Thus, an evaluation of any one of the functions φ, 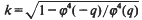 [1, p. 102].)
[1, p. 102].)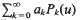 given by
given by 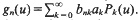 . We establish necessary and sufficient conditions on the matrix (
. We establish necessary and sufficient conditions on the matrix (