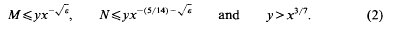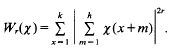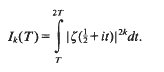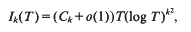Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
Preface
-
-
- Book:
- Surveys in Combinatorics, 1995
- Published online:
- 05 May 2010
- Print publication:
- 20 July 1995, pp vii-viii
-
- Chapter
- Export citation
The value set of polynomials over ℤm and the combinatorics of sequences
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 190-198
- Print publication:
- June 1995
-
- Article
- Export citation
Inherited group actions on ℝ-trees
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 206-213
- Print publication:
- June 1995
-
- Article
- Export citation
M. Auslander, I. Reiten and S. O. Smalø. Representation Theory of Artin Algebras. Cambridge University Press. 1995, ISBN 0 521 41134 3, 423 pp., £50. - M. J. Baines. Moving Finite Elements. Clarendon Press. 1994, ISBN 0 19 853467 1, 226 pp., £45. - F. Borceux. Handbook of Categorical Algebra, I. Basic Category Theory. II. Categories and Structures. Encyclopedia of Mathematics and its Applications, 50, 51. Cambridge University Press. 1994, Vol. I, ISBN 0 521 44178 1, Vol. II, ISBN 0 521 44179 X, 345 pp., 443 pp., £45, £50. - H. J. M. Bos. Lectures in the History of Mathematics. AMS/LMS. 1993, ISBN 0 8218 9001 8, 197 pp., £71. - P. M. Cohn. Elements of Linear Algebra. Chapman and Hall. 1994, ISBN 0 412 55280 9, 226 pp., paperback, £13·99. - J. Dauns. Modules and Rings. Cambridge University Press. 1994, ISBN 0 521 46258 4, 442 pp., £45. - W. Dunham. The Mathematical Universe. Wiley. 1994, ISBN 0 471 53656 3, 314 pp., £16·95. - N. D. Gilbert and T. Porter. Knots and Surfaces. Oxford University Press. 1994, ISBN 0 19 853397 7, 268 pp., £29·50. - P. Griffiths and J. Harris. Principles of Algebraic Geometry. Wiley. 1994, ISBN 0 471 05059 8, 813 pp., £30·50. - W. K. Hayman. Multivalent Functions, 2nd Ed., Cambridge Tracts in Mathematics, Vol. 110. Cambridge University Press. 1994, ISBN 0 521 46026 3, 263 pp., £35. - W. V. D. Hodge and D. Pedoe. Methods of Algebraic Geometry, Vol. 1. Cambridge University Press. 1994, ISBN 0 521 469007 4, 440 pp., paperback, £14·95. - K. W. Morton and D. F. Mayers. Numerical Solution of Partial Differential Equations. Cambridge University Press. 1994, hardback ISBN 0 521 418550 0, paperback ISBN 0 521 42922 6, 227 pp., hardback, £35, paperback, £13·95. - J. D. Murray. Mathematical Biology, 2nd Ed. Springer. 1993, ISBN 3 540 57204 X, 767 pp., DM 68. - K. Nomizu and T. Sasaki. Affine differential Geometry. Cambridge University Press. 1994, ISBN 0 521 44177 3, 263 pp., £35. - J.-P. Pier, Editor. Development of Mathematics, 1900–1950. Birkhäuser. 1994, ISBN 3 7643 2821 5, 729 pp., £43. - M. Rahman. Water Waves. Relating Modern Theory to Advanced Engineering Practice. Clarendon Press. 1994, ISBN 0 19 853478 7, 343 pp., £50. - M. Rosenblum and J. Rovnyak. Topics in Hardy Classes and Univalent Functions. Birkhaüser. 1994, ISBN 3 7643 5111 X, 250 pp., £36. - I. R. Shafarevich. Basic Algebraic Geometry. Vol. I, Varieties in Projective Space. Vol. II, Schemes and Complex Manifolds. Springer. 1994, Vol. I, ISBN 3 540 54812 2, 303 pp., 68 DM, Vol. II, ISBN 3 540 57554 5, 269 pp., 68 DM. - D. Stoyan and H. Stoyan. Fractals, Random Shapes and Point Fields. Wiley. 1994, ISBN 0 471 93757 6, 389 pp., £39·95. - K. R. Stromberg. Probability for Analysts. Chapman and Hall. 1994, ISBN 0 412 04171 5, 330 pp., £49. - R. Torretti. Philosophy of geometry from Riemann to Poincaré. Reidel. 1994, ISBN 9 027 70920 3, 459 pp., £34. - N. J. Vilenkin and A. U. Klimyk. Representation of Lie Groups and Special Functions. Vol. 2, Class I Representations, Special Functions and Integral Transforms. Kluwer. 1993, ISBN 0 7923 1492 1, 607 pp., £183. - S. Zdravkovska and P. L. Duren, Editors. Golden Years of Moscow Mathematics. AMS/LMS. 1993, ISBN 0 8218 9003 4, 271 pp., £78.
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 222-227
- Print publication:
- June 1995
-
- Article
- Export citation
A note on Stokes flow due to a line rotlet
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-132
- Print publication:
- June 1995
-
- Article
- Export citation
Bounding a unit index in terms of a ring index
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 199-205
- Print publication:
- June 1995
-
- Article
- Export citation
A generic factorization theorem
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 56-66
- Print publication:
- June 1995
-
- Article
- Export citation
The rotation of two circular cylinders in a viscous fluid
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 105-126
- Print publication:
- June 1995
-
- Article
- Export citation
On the existence of subsets of finite positive packing measure
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 15-24
- Print publication:
- June 1995
-
- Article
- Export citation
On Cesaro summable sequences of continuous functions
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 87-104
- Print publication:
- June 1995
-
- Article
- Export citation
Corrigenda to “Random Banach spaces: the limitations of the method”
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 220-221
- Print publication:
- June 1995
-
- Article
- Export citation
Order-two density of sets and measures with non-integral dimension
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-14
- Print publication:
- June 1995
-
- Article
- Export citation
A special triple exponential sum
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 137-143
- Print publication:
- June 1995
-
- Article
- Export citation
Recovering Baire 1 functions
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 43-48
- Print publication:
- June 1995
-
- Article
- Export citation
Mean values of character sums III
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 133-136
- Print publication:
- June 1995
-
- Article
- Export citation
Mean-values of the Riemann zeta-function
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 158-174
- Print publication:
- June 1995
-
- Article
- Export citation
A lattice without a basis of minimal vectors
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 175-177
- Print publication:
- June 1995
-
- Article
- Export citation
Baire trees, bad norms and the Namioka property
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 30-42
- Print publication:
- June 1995
-
- Article
- Export citation
MTK volume 42 issue 1 Cover and Front matter
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
- Print publication:
- June 1995
-
- Article
-
- You have access
- Export citation
Infima of hyperspace topologies
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 67-86
- Print publication:
- June 1995
-
- Article
- Export citation
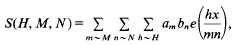
 ,
,