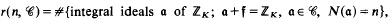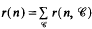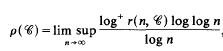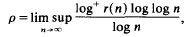Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
“Turán Type Problems”
-
-
- Book:
- Surveys in Combinatorics, 1991
- Published online:
- 05 September 2013
- Print publication:
- 22 August 1991, pp 253-300
-
- Chapter
- Export citation
5 - Some Special Graphs
-
- Book:
- Combinatorial Matrix Theory
- Published online:
- 05 May 2013
- Print publication:
- 26 July 1991, pp 145-163
-
- Chapter
- Export citation
7 - The Permanent
-
- Book:
- Combinatorial Matrix Theory
- Published online:
- 05 May 2013
- Print publication:
- 26 July 1991, pp 198-249
-
- Chapter
- Export citation
Master Reference List
-
- Book:
- Combinatorial Matrix Theory
- Published online:
- 05 May 2013
- Print publication:
- 26 July 1991, pp 345-362
-
- Chapter
- Export citation
3 - Matrices and Digraphs
-
- Book:
- Combinatorial Matrix Theory
- Published online:
- 05 May 2013
- Print publication:
- 26 July 1991, pp 53-106
-
- Chapter
- Export citation
1 - Incidence Matrices
-
- Book:
- Combinatorial Matrix Theory
- Published online:
- 05 May 2013
- Print publication:
- 26 July 1991, pp 1-22
-
- Chapter
- Export citation
9 - Combinatorial Matrix Algebra
-
- Book:
- Combinatorial Matrix Theory
- Published online:
- 05 May 2013
- Print publication:
- 26 July 1991, pp 291-344
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Combinatorial Matrix Theory
- Published online:
- 05 May 2013
- Print publication:
- 26 July 1991, pp i-iv
-
- Chapter
- Export citation
2 - Matrices and Graphs
-
- Book:
- Combinatorial Matrix Theory
- Published online:
- 05 May 2013
- Print publication:
- 26 July 1991, pp 23-52
-
- Chapter
- Export citation
6 - Existence Theorems
-
- Book:
- Combinatorial Matrix Theory
- Published online:
- 05 May 2013
- Print publication:
- 26 July 1991, pp 164-197
-
- Chapter
- Export citation
Contents
-
- Book:
- Combinatorial Matrix Theory
- Published online:
- 05 May 2013
- Print publication:
- 26 July 1991, pp v-vi
-
- Chapter
- Export citation
Index
-
- Book:
- Combinatorial Matrix Theory
- Published online:
- 05 May 2013
- Print publication:
- 26 July 1991, pp 363-367
-
- Chapter
- Export citation
Preface
-
-
- Book:
- Combinatorial Matrix Theory
- Published online:
- 05 May 2013
- Print publication:
- 26 July 1991, pp vii-x
-
- Chapter
- Export citation
8 - Latin Squares
-
- Book:
- Combinatorial Matrix Theory
- Published online:
- 05 May 2013
- Print publication:
- 26 July 1991, pp 250-290
-
- Chapter
- Export citation
4 - Matrices and Bipartite Graphs
-
- Book:
- Combinatorial Matrix Theory
- Published online:
- 05 May 2013
- Print publication:
- 26 July 1991, pp 107-144
-
- Chapter
- Export citation
MTK volume 38 issue 1 Cover and Front matter
-
- Journal:
- Mathematika / Volume 38 / Issue 1 / June 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
- Print publication:
- June 1991
-
- Article
-
- You have access
- Export citation
A note on radial variation of analytic functions
-
- Journal:
- Mathematika / Volume 38 / Issue 1 / June 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 191-193
- Print publication:
- June 1991
-
- Article
- Export citation
Mosco convergence and weak topologies for convex sets and functions
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 1 / June 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-104
- Print publication:
- June 1991
-
- Article
- Export citation
Some explicit continued fraction expansions
-
- Journal:
- Mathematika / Volume 38 / Issue 1 / June 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
- Print publication:
- June 1991
-
- Article
- Export citation
On the number of integral ideals of given norm and ray-class
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 1 / June 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 185-190
- Print publication:
- June 1991
-
- Article
- Export citation