Refine search
Actions for selected content:
9084 results in Discrete Mathematics, Information Theory and Coding
The magnetic field perturbations produced by an ellipsoidal cavity in a uniform conductor
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 247-255
- Print publication:
- December 1988
-
- Article
- Export citation
Tauberian theorems for Jakimovski and Karamata-Stirling methods
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 216-224
- Print publication:
- December 1988
-
- Article
- Export citation
A generalization of mixed invariant sets
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 198-206
- Print publication:
- December 1988
-
- Article
- Export citation
Systems of parameters for non-finitely generated modules and big Cohen–Macaulay modules
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 207-215
- Print publication:
- December 1988
-
- Article
- Export citation
Distribution of rational points on varieties over finite fields
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 155-171
- Print publication:
- December 1988
-
- Article
- Export citation
Convex bodies, economic cap coverings, random polytopes
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 274-291
- Print publication:
- December 1988
-
- Article
- Export citation
Asymptotic theory for third-order differential equations
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 225-232
- Print publication:
- December 1988
-
- Article
- Export citation
The exact length of the Euclidean algorithm in
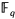 [X]
[X]
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 297-304
- Print publication:
- December 1988
-
- Article
- Export citation
Index to Volume 35
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, p. 309
- Print publication:
- December 1988
-
- Article
- Export citation
MTK volume 35 issue 2 Cover and Front matter
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
- Print publication:
- December 1988
-
- Article
-
- You have access
- Export citation
On packings and coverings of unit density
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 172-179
- Print publication:
- December 1988
-
- Article
- Export citation
The fractional parts of a smooth sequence
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 292-296
- Print publication:
- December 1988
-
- Article
- Export citation
Book Reviews - G. E. Andrews, R. A. Askey, B. C. Berndt, K. G. Ramanathan and R. A. Rankin, Editors. Ramanujan revisited. Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign, June, 1–5, 1987. Academic Press. 1988, 609 pp., $49·50. - M. F. Atiyah. Collected works, Vol. I: Early papers: General papers. Clarendon Press. 1988, 364 pp., £30. - H. Busemann and B. B. Phadke. Spaces with distinguished geodesics. Marcel Dekker. 1987, 159 pp., $49·75. - Centre National de la Recherche Scientifique. Analyse mathématique et applications. Gauthier-Villars. 1988, 503 pp., 295 FF. - P. J. Davis and R. Hersch. Descartes' Dream. Penguin Books. 1988, 321 pp., £8·95. - K. Devlin. Mathematics: The new golden age. Penguin Books. 1988, 287 pp., £7·95. - I. Ekeland. Mathematics and the unexpected (Author's translation of the 1984 French original). University of Chicago Press. 1988, 146 pp., £15·96. - J. M. G. Fell and R. S. Doran. Representations of *-algebras, locally compact groups and Banach *-algebraic bundles. Academic Press. 1988, two volumes, 1,486 pp., $99 per volume. - P. Günther. Huygens' principle and hyperbolic equations. Perspectives in mathematics, Vol. 5. Academic Press. 1988, 847 pp., $69. - G. Higman and E. Scott. Existentially closed groups. Clarendon Press. 1988, 156 pp., £25. - S. Łojasiewicz. An introduction to the theory of real functions. Wiley. 1988, 230 pp., £24·95. - S. MacLane and G. Birkhoff. Algebra, 3rd Edition. Chelsea. 1988, 626 pp., £28·50. - J. E. Marsden and A. J. Tromba. Vector calculus. Freeman. 1988, 655 pp., £29·95. - Y. Matsumoto, T. Mizutani and S. Morita, Editors. A fête of topology: Papers dedicated to Itiro Tamura. Academic Press. 1988, 602 pp., £37·50. - F. Morgan. Geometric measure theory: A beginner's guide. Academic Press. 1988, 145 pp., $50·00. - J. A. Rice. Mathematical statistics and data analysis. Wadsworth. 1988, 594 pp., £15·95. - H. E. Rose. A course in number theory. Clarendon Press. 1988, 354 pp., £40 hardback, £17·50 paperback. - L. H. Rowen. Ring theory. Academic Press. 1988, Vol. I, 538 pp., $89·50, Vol. II, 462 pp., $84·00. - N. M. Stephens and M. P. Thorne, Editors. Computers in mathematical research. Conference series of the Institute of Mathematics and its Applications. Clarendon Press. 1988, 251 pp., £25. - C. J. Thompson. Classical equilibrium statistical mechanics. Clarendon Press. 1988, 213 pp., £20.
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 305-308
- Print publication:
- December 1988
-
- Article
- Export citation
Some Stokes flows exterior to a spherical boundary
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 233-246
- Print publication:
- December 1988
-
- Article
- Export citation
Finite-time break-up can occur in any unsteady interacting boundary layer
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 256-273
- Print publication:
- December 1988
-
- Article
- Export citation
Introduction
-
-
- Book:
- Algebraic, Extremal and Metric Combinatorics 1986
- Published online:
- 05 April 2013
- Print publication:
- 25 August 1988, pp vii-vii
-
- Chapter
- Export citation
Geometric Methods in Group Theory
-
-
- Book:
- Algebraic, Extremal and Metric Combinatorics 1986
- Published online:
- 05 April 2013
- Print publication:
- 25 August 1988, pp 219-237
-
- Chapter
- Export citation
Some Recent Combinatorial Applications of Borsuk-Type Theorems
-
-
- Book:
- Algebraic, Extremal and Metric Combinatorics 1986
- Published online:
- 05 April 2013
- Print publication:
- 25 August 1988, pp 1-12
-
- Chapter
- Export citation
Metric and Geometric Properties of Sets of Permutations
-
-
- Book:
- Algebraic, Extremal and Metric Combinatorics 1986
- Published online:
- 05 April 2013
- Print publication:
- 25 August 1988, pp 39-53
-
- Chapter
- Export citation
Intersection and Containment Problems Without Size Restrictions
-
-
- Book:
- Algebraic, Extremal and Metric Combinatorics 1986
- Published online:
- 05 April 2013
- Print publication:
- 25 August 1988, pp 62-111
-
- Chapter
- Export citation
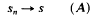
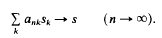
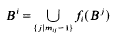
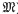 ) be a commutative Noetherian local ring. We investigate conditions for a non-finitely generated
) be a commutative Noetherian local ring. We investigate conditions for a non-finitely generated 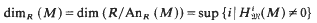
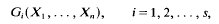
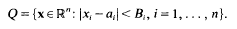
 [
[