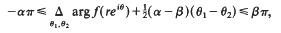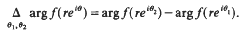Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
CHAPTER VIII - EXTENDED UNIQUENESS SETS
-
- Book:
- Descriptive Set Theory and the Structure of Sets of Uniqueness
- Published online:
- 07 September 2010
- Print publication:
- 27 November 1987, pp 266-308
-
- Chapter
- Export citation
CHAPTER VII - THE SHRINKING METHOD, THE THEOREM OF KÖRNER AND KAUFMAN, AND THE SOLUTION TO THE BOREL BASIS PROBLEM FOR U
-
- Book:
- Descriptive Set Theory and the Structure of Sets of Uniqueness
- Published online:
- 07 September 2010
- Print publication:
- 27 November 1987, pp 231-265
-
- Chapter
- Export citation
CHAPTER I - TRIGONOMETRIC SERIES AND SETS OF UNIQUENESS
-
- Book:
- Descriptive Set Theory and the Structure of Sets of Uniqueness
- Published online:
- 07 September 2010
- Print publication:
- 27 November 1987, pp 21-50
-
- Chapter
- Export citation
8 - Whitney Numbers
-
-
- Book:
- Combinatorial Geometries
- Published online:
- 05 May 2013
- Print publication:
- 24 September 1987, pp 139-160
-
- Chapter
- Export citation
Preface
-
-
- Book:
- Combinatorial Geometries
- Published online:
- 05 May 2013
- Print publication:
- 24 September 1987, pp xi-xii
-
- Chapter
- Export citation
3 - Unimodular Matroids
-
-
- Book:
- Combinatorial Geometries
- Published online:
- 05 May 2013
- Print publication:
- 24 September 1987, pp 40-52
-
- Chapter
- Export citation
Contents
-
- Book:
- Combinatorial Geometries
- Published online:
- 05 May 2013
- Print publication:
- 24 September 1987, pp v-viii
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Combinatorial Geometries
- Published online:
- 05 May 2013
- Print publication:
- 24 September 1987, pp i-iv
-
- Chapter
- Export citation
List of Contributors
-
- Book:
- Combinatorial Geometries
- Published online:
- 05 May 2013
- Print publication:
- 24 September 1987, pp ix-ix
-
- Chapter
- Export citation
7 - The Möbius Function and the Characteristic Polynomial
-
-
- Book:
- Combinatorial Geometries
- Published online:
- 05 May 2013
- Print publication:
- 24 September 1987, pp 114-138
-
- Chapter
- Export citation
2 - Binary Matroids
-
-
- Book:
- Combinatorial Geometries
- Published online:
- 05 May 2013
- Print publication:
- 24 September 1987, pp 28-39
-
- Chapter
- Export citation
Index
-
- Book:
- Combinatorial Geometries
- Published online:
- 05 May 2013
- Print publication:
- 24 September 1987, pp 211-212
-
- Chapter
- Export citation
6 - Simplicial Matroids
-
-
- Book:
- Combinatorial Geometries
- Published online:
- 05 May 2013
- Print publication:
- 24 September 1987, pp 98-113
-
- Chapter
- Export citation
4 - Introduction to Matching Theory
-
-
- Book:
- Combinatorial Geometries
- Published online:
- 05 May 2013
- Print publication:
- 24 September 1987, pp 53-71
-
- Chapter
- Export citation
9 - Matroids in Combinatorial Optimization
-
-
- Book:
- Combinatorial Geometries
- Published online:
- 05 May 2013
- Print publication:
- 24 September 1987, pp 161-210
-
- Chapter
- Export citation
5 - Transversal Matroids
-
-
- Book:
- Combinatorial Geometries
- Published online:
- 05 May 2013
- Print publication:
- 24 September 1987, pp 72-97
-
- Chapter
- Export citation
1 - Coordinatizations
-
-
- Book:
- Combinatorial Geometries
- Published online:
- 05 May 2013
- Print publication:
- 24 September 1987, pp 1-27
-
- Chapter
- Export citation
Series Editor's Statement
-
-
- Book:
- Combinatorial Geometries
- Published online:
- 05 May 2013
- Print publication:
- 24 September 1987, pp x-x
-
- Chapter
- Export citation
A gap condition for the zeroes of certain polynomials in Kaplan classes K(α, β)
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 1 / June 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 53-63
- Print publication:
- June 1987
-
- Article
- Export citation
Existence and stability in convection in porous media
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 1 / June 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-52
- Print publication:
- June 1987
-
- Article
- Export citation