Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
Isoperimetric problems for tilings, corrigendum
-
- Journal:
- Mathematika / Volume 33 / Issue 2 / December 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 189-191
- Print publication:
- December 1986
-
- Article
- Export citation
An upper estimate for the lattice point enumerator
-
- Journal:
- Mathematika / Volume 33 / Issue 2 / December 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 197-203
- Print publication:
- December 1986
-
- Article
- Export citation
Angle-sum relations for polyhedral sets
-
- Journal:
- Mathematika / Volume 33 / Issue 2 / December 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 173-188
- Print publication:
- December 1986
-
- Article
- Export citation
d-sequences, local cohomology modules and generalized analytic independence
- Part of
-
- Journal:
- Mathematika / Volume 33 / Issue 2 / December 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 279-284
- Print publication:
- December 1986
-
- Article
- Export citation
On generalized Dedekind domains
- Part of
-
- Journal:
- Mathematika / Volume 33 / Issue 2 / December 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 285-295
- Print publication:
- December 1986
-
- Article
- Export citation
MTK volume 33 issue 2 Cover and Front matter
-
- Journal:
- Mathematika / Volume 33 / Issue 2 / December 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f3
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Index of subjects
-
- Book:
- Some Topics in Graph Theory
- Published online:
- 19 March 2010
- Print publication:
- 17 July 1986, pp 228-229
-
- Chapter
- Export citation
Chapter 1 - Basic Terminology
-
- Book:
- Some Topics in Graph Theory
- Published online:
- 19 March 2010
- Print publication:
- 17 July 1986, pp 1-8
-
- Chapter
- Export citation
Introduction
-
- Book:
- Some Topics in Graph Theory
- Published online:
- 19 March 2010
- Print publication:
- 17 July 1986, pp v-vi
-
- Chapter
- Export citation
Chapter 3 - Symmetries in Graphs
-
- Book:
- Some Topics in Graph Theory
- Published online:
- 19 March 2010
- Print publication:
- 17 July 1986, pp 88-155
-
- Chapter
- Export citation
Index of notation
-
- Book:
- Some Topics in Graph Theory
- Published online:
- 19 March 2010
- Print publication:
- 17 July 1986, pp 230-230
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Some Topics in Graph Theory
- Published online:
- 19 March 2010
- Print publication:
- 17 July 1986, pp i-iv
-
- Chapter
- Export citation
Contents
-
- Book:
- Some Topics in Graph Theory
- Published online:
- 19 March 2010
- Print publication:
- 17 July 1986, pp vii-viii
-
- Chapter
- Export citation
Chapter 2 - Edge–colourings of Graphs
-
- Book:
- Some Topics in Graph Theory
- Published online:
- 19 March 2010
- Print publication:
- 17 July 1986, pp 9-87
-
- Chapter
- Export citation
Chapter 5 - Computational Complexity of Graph Properties
-
- Book:
- Some Topics in Graph Theory
- Published online:
- 19 March 2010
- Print publication:
- 17 July 1986, pp 196-227
-
- Chapter
- Export citation
Chapter 4 - Packing of Graphs
-
- Book:
- Some Topics in Graph Theory
- Published online:
- 19 March 2010
- Print publication:
- 17 July 1986, pp 156-195
-
- Chapter
- Export citation
Sphere packing in R3
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 137-147
- Print publication:
- June 1986
-
- Article
- Export citation
On the large sieve inequality in an algebraic number field
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 31-54
- Print publication:
- June 1986
-
- Article
- Export citation
Book Reviews - E. Bach. Analytic Methods in the Analysis and Design of Number Theoretic Algorithms. The MIT Press. 1985, 62 pp., £14·95. - C. A. Baker and L. M. Batten, Editors. Finite Geometries. Marcel Dekker. 1985, 387 pp., $83·50. - J. Berstel and D. Perrin. Theory of Codes. Academic Press. 1985, 447 pp., £60·00. - B. Bollobás. Random Graphs. Academic Press. 1985, 447 pp., £52·00. - M. R. Cullen. Linear Models in Biology. Ellis Horwood. 1985, 213 pp., £10·50. - J. I. Diaz. Nonlinear Partial Differential Equations and Free Boundaries, Volume I, Elliptic Equations. Pitman Adv. Publ. Program. 1985, 331pp., £18·50. - C.-E. Fröberg. Numerical Mathematics: Theory and Computer Applications. Benjamin Cummings Publ. 1985, 448pp., £15·95. - R. Geroch. Mathematical Physics. University of Chicago Press. 1986, 357pp., £25·00 (c), £12·75 (p). - R.-E. Hoffmann and K. H. Hofmann, Editors. Continuous Lattices and their Applications. Marcel Dekker. 1985, 379pp., $83·50. - A. S. Lodge et al., Editors. Viscoelasticity and Rheology. Proc. Symp. Wisconsin, 1984. Academic Press. 1985, 455pp., £31·50. - L. Narici and E. Beckenstein. Topological Vector Spaces. Marcel Dekker. 1985, 419pp., $83·50. - W. B. Powell and C. Tsinakis, Editors. Ordered Algebraic Structures. Marcel Dekker. 1985, 208pp., $59·50. - G. M. Rassias and T. M. Rassias. Editors. Differential Geometry, Calculus of Variations, and their Applications. Marcel Dekker. 1985, 536pp., $90·00. - M. Rosenblum and J. Rovnyak. Hardy Classes and Operator Theory. Oxford University Press. 1985, 175pp., £37·50. - R. J. Wilson. Introduction to Graph Theory, Third Edition. Longman. 1985, 174pp., £5·95. (Hints and Solutions Manual. £2·95).
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 170-172
- Print publication:
- June 1986
-
- Article
- Export citation
MTK volume 33 issue 1 Cover and Front matter
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
- Print publication:
- June 1986
-
- Article
-
- You have access
- Export citation
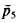 and
and 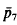 , and ā
, and ā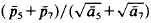 was equal to 3.7263… This being greater than √8√3 = 3–7224… the tiling given in [1] does not yield the desired counter-example. In what follows we shall construct a tiling for which the respective quotient will turn out to be less than √8√3.
was equal to 3.7263… This being greater than √8√3 = 3–7224… the tiling given in [1] does not yield the desired counter-example. In what follows we shall construct a tiling for which the respective quotient will turn out to be less than √8√3. to denote, for
to denote, for