Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
The distribution of r-tuples of square-free numbers
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 265-275
- Print publication:
- December 1985
-
- Article
- Export citation
Pairs of additive congruences: cubic congruences
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 286-300
- Print publication:
- December 1985
-
- Article
- Export citation
On the temperature of radial bearings. 1
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 317-323
- Print publication:
- December 1985
-
- Article
- Export citation
MTK volume 32 issue 2 Cover and Front matter
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1985
-
- Article
-
- You have access
- Export citation
Espaces К-analytiques et espaces de Baire de fonctions continues
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 218-228
- Print publication:
- December 1985
-
- Article
- Export citation
Pairs of primitive roots
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 276-285
- Print publication:
- December 1985
-
- Article
- Export citation
Lattice covering of space with symmetric convex bodies
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 311-315
- Print publication:
- December 1985
-
- Article
- Export citation
Borel selectors for upper semi-continuous multi-valued functions
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 324-337
- Print publication:
- December 1985
-
- Article
- Export citation
Holomorphically parameterized families of subgroups of sl(2, ℂ)
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 248-264
- Print publication:
- December 1985
-
- Article
- Export citation
Classes of sets with large intersection
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 191-205
- Print publication:
- December 1985
-
- Article
- Export citation
Chapter 3 - Some Related Problems
-
- Book:
- Results and Problems in Combinatorial Geometry
- Published online:
- 23 October 2009
- Print publication:
- 10 October 1985, pp 69-95
-
- Chapter
- Export citation
Foreword
-
- Book:
- Results and Problems in Combinatorial Geometry
- Published online:
- 23 October 2009
- Print publication:
- 10 October 1985, pp vii-viii
-
- Chapter
- Export citation
Chapter 1 - Partition of a set into sets of smaller diameter
-
- Book:
- Results and Problems in Combinatorial Geometry
- Published online:
- 23 October 2009
- Print publication:
- 10 October 1985, pp 1-34
-
- Chapter
- Export citation
Biblography
-
- Book:
- Results and Problems in Combinatorial Geometry
- Published online:
- 23 October 2009
- Print publication:
- 10 October 1985, pp 107-108
-
- Chapter
- Export citation
Contents
-
- Book:
- Results and Problems in Combinatorial Geometry
- Published online:
- 23 October 2009
- Print publication:
- 10 October 1985, pp v-vi
-
- Chapter
- Export citation
Chapter 2 - The covering of convex bodies with homothetic bodies and the illumination problem
-
- Book:
- Results and Problems in Combinatorial Geometry
- Published online:
- 23 October 2009
- Print publication:
- 10 October 1985, pp 35-68
-
- Chapter
- Export citation
Introduction to the English edition
-
- Book:
- Results and Problems in Combinatorial Geometry
- Published online:
- 23 October 2009
- Print publication:
- 10 October 1985, pp ix-x
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Results and Problems in Combinatorial Geometry
- Published online:
- 23 October 2009
- Print publication:
- 10 October 1985, pp i-iv
-
- Chapter
- Export citation
Notes
-
- Book:
- Results and Problems in Combinatorial Geometry
- Published online:
- 23 October 2009
- Print publication:
- 10 October 1985, pp 96-106
-
- Chapter
- Export citation
Contents
-
- Book:
- Surveys in Combinatorics 1985
- Published online:
- 05 May 2013
- Print publication:
- 25 July 1985, pp v-v
-
- Chapter
- Export citation
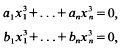
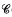
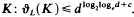 . Here,
. Here, 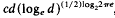 , which is, of course a major improvement. In the present paper we show that such an improvement can be obtained for a larger class of convex bodies. In particular, we prove the following theorem. Let
, which is, of course a major improvement. In the present paper we show that such an improvement can be obtained for a larger class of convex bodies. In particular, we prove the following theorem. Let 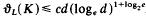 . Actually, for a bound of this type we do not even need any symmetry assumption. In fact, some weaker properties concerning shadow boundaries will suffice.
. Actually, for a bound of this type we do not even need any symmetry assumption. In fact, some weaker properties concerning shadow boundaries will suffice.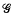 be a finitely generated subgroup of SL (2, ℱ), where ℱ is the ring; of holomorphic functions on the open unit disc Δ. For each point
be a finitely generated subgroup of SL (2, ℱ), where ℱ is the ring; of holomorphic functions on the open unit disc Δ. For each point 