Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
Extending classical criteria for differentiation theorems
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 1 / June 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 68-74
- Print publication:
- June 1985
-
- Article
- Export citation
Isoperimetric problems for tilings
-
- Journal:
- Mathematika / Volume 32 / Issue 1 / June 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-15
- Print publication:
- June 1985
-
- Article
- Export citation
The asymptotic solution of linear differential systems
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 1 / June 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-138
- Print publication:
- June 1985
-
- Article
- Export citation
Cohomology of Bieberbach groups
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 1 / June 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 55-59
- Print publication:
- June 1985
-
- Article
- Export citation
A note on the integral points of a modular curve of level 7
-
- Journal:
- Mathematika / Volume 32 / Issue 1 / June 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 45-48
- Print publication:
- June 1985
-
- Article
- Export citation
Functions and measures on products spaces
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 1 / June 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 60-67
- Print publication:
- June 1985
-
- Article
- Export citation
The distribution of exponential sums
-
- Journal:
- Mathematika / Volume 32 / Issue 1 / June 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 16-25
- Print publication:
- June 1985
-
- Article
- Export citation
An upper bound for the index of χ-irregularity
-
- Journal:
- Mathematika / Volume 32 / Issue 1 / June 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-44
- Print publication:
- June 1985
-
- Article
- Export citation
Convex bodies equidecomposable by locally discrete groups of isometries
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 1 / June 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
- Print publication:
- June 1985
-
- Article
- Export citation
Perturbation theory for a displacement front passing discontinuities in capillary pressure and permeability in a porous medium
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 1 / June 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 75-89
- Print publication:
- June 1985
-
- Article
- Export citation
Separation of K–analytic sets
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 1 / June 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 147-190
- Print publication:
- June 1985
-
- Article
- Export citation
6 - Other 2-designs
-
- Book:
- Design Theory
- Published online:
- 08 January 2010
- Print publication:
- 27 May 1985, pp 173-184
-
- Chapter
- Export citation
Index
-
- Book:
- Design Theory
- Published online:
- 08 January 2010
- Print publication:
- 27 May 1985, pp 238-240
-
- Chapter
- Export citation
4 - 3-Designs and related topics
-
- Book:
- Design Theory
- Published online:
- 08 January 2010
- Print publication:
- 27 May 1985, pp 127-152
-
- Chapter
- Export citation
5 - Resolutions
-
- Book:
- Design Theory
- Published online:
- 08 January 2010
- Print publication:
- 27 May 1985, pp 153-172
-
- Chapter
- Export citation
2 - Symmetric designs
-
- Book:
- Design Theory
- Published online:
- 08 January 2010
- Print publication:
- 27 May 1985, pp 52-82
-
- Chapter
- Export citation
3 - Some families of symmetric designs
-
- Book:
- Design Theory
- Published online:
- 08 January 2010
- Print publication:
- 27 May 1985, pp 83-126
-
- Chapter
- Export citation
Introduction
-
- Book:
- Design Theory
- Published online:
- 08 January 2010
- Print publication:
- 27 May 1985, pp vii-viii
-
- Chapter
- Export citation
7 - Some 1-designs
-
- Book:
- Design Theory
- Published online:
- 08 January 2010
- Print publication:
- 27 May 1985, pp 185-211
-
- Chapter
- Export citation
List of abbreviations
-
- Book:
- Design Theory
- Published online:
- 08 January 2010
- Print publication:
- 27 May 1985, pp 237-237
-
- Chapter
- Export citation
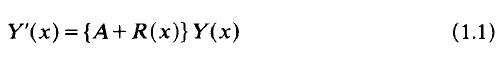
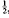 , the following theorem holds.
, the following theorem holds.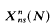 . denote the modular curve associated with the normalizer of a non-split Cartan group of level
. denote the modular curve associated with the normalizer of a non-split Cartan group of level 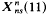 has genus 1. Ligozat [5] has shown that the group of Q-rational points on
has genus 1. Ligozat [5] has shown that the group of Q-rational points on 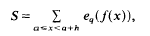
 analytic sets developed by Stone and Hansell. As we explain in [5], this theory parallels the recently developed theory of Frolík and Holický, but has certain advantages. In this paper we take the theory rather further, and, in particular, we prove a number of variants of Lusin's first separation theorem and give some of their applications. We make free use of the definitions, notation and conventions introduced in [5].
analytic sets developed by Stone and Hansell. As we explain in [5], this theory parallels the recently developed theory of Frolík and Holický, but has certain advantages. In this paper we take the theory rather further, and, in particular, we prove a number of variants of Lusin's first separation theorem and give some of their applications. We make free use of the definitions, notation and conventions introduced in [5].