Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
Index
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp 313-316
-
- Chapter
- Export citation
Chapter 9 - Weak Maps
-
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp 254-271
-
- Chapter
- Export citation
Chapter 5 - Orthogonality
-
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp 76-96
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp i-iv
-
- Chapter
- Export citation
Chapter 8 - Strong Maps
-
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp 224-253
-
- Chapter
- Export citation
Chapter 4 - Basis-Exchange Properties
-
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp 62-75
-
- Chapter
- Export citation
Chapter 7 - Constructions
-
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp 127-223
-
- Chapter
- Export citation
Series Editor's Statement
-
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp xi-xii
-
- Chapter
- Export citation
Chapter 1 - Examples and Basic Concepts
-
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp 1-28
-
- Chapter
- Export citation
Chapter 10 - Semimodular Functions
-
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp 272-297
-
- Chapter
- Export citation
Foreword
-
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp xiii-xiv
-
- Chapter
- Export citation
Chapter 2 - Axiom Systems
-
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp 29-44
-
- Chapter
- Export citation
Chapter 3 - Lattices
-
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp 45-61
-
- Chapter
- Export citation
Piece-wise closed functions and almost discretely σ-decomposable families
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 229-247
- Print publication:
- December 1985
-
- Article
- Export citation
Index to Volume 32
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, p. 340
- Print publication:
- December 1985
-
- Article
- Export citation
On the Hausdorff dimensions of distance sets
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 206-212
- Print publication:
- December 1985
-
- Article
- Export citation
On the Hausdorff dimension and capacities of intersections
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 213-217
- Print publication:
- December 1985
-
- Article
- Export citation
Diophantine approximation with almost-primes and sums of two squares
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 301-310
- Print publication:
- December 1985
-
- Article
- Export citation
Book Reviews - S. Albeverio, Editor. Infinite-dimensional analysis and stochastic processes. Pitman Adv. Publ. Program. 1985, 256pp., £16·50. - A. Boissavit, A. Damlamian and M. Fremond, Editors. Free Boundary Problems: Application and Theory. Pitman Adv. Publ. Program. 1985, vol III, 315pp. and vol IV, 321pp., each volume £18·50. - H. Brezis and J. L. Lions, Editors. Nonlinear partial differential equations and their applications. Collège de France Seminar, vol VII. Pitman Adv. Publ. Program. 1985, 300pp., £16·50. - L. A. Cordero, Editor. Differential Geometry. Pitman Adv. Publ. Program. 1985, 355pp. - Hua Loo Keng, Lin Wei and Wu Ci-Quian. Second-order systems of partial differential equations in the plane. Pitman Adv. Publ. Program. 1985, 300pp., £16·50. - N. Jacobson. Basic Algebra I. Second edition. W. H. Freeman. 1985, 517pp., £19·95. - C. L. Liu. Elements of Discrete Mathematics. Second edition. McGraw-Hill. 1985, 447pp., £47·50. - J. D. P. Meldrum. Near-rings and their links with groups. Pitman Adv. Publ. Program. 1985, 287pp., £16·50. - R. D. Nussbaum. The Fixed Point Index and Some Applications. L'Université de Montréal. 1985, 145pp., Canadian $18·00. - L. Schwartz. Semimartingales and their Stochastic Calculus on Manifolds. L'Université de Montreal. 1984, 187pp., Canadian $17·00. - D. Shanks. Solved and Unsolved Problems in Number Theory. 3rd edition. Chelsea. 1985, 318pp., $18·95. - R. Wu. Stochastic Differential Equations. Pitman Adv. Publ. Program. 1985, 149pp., £12·50.
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 338-339
- Print publication:
- December 1985
-
- Article
- Export citation
On torsion of abelian varieties over large algebraic extensions of finitely generated fields: Erratum
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, p. 316
- Print publication:
- December 1985
-
- Article
-
- You have access
- Export citation
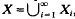 with each set
with each set