Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
The delay differential equation
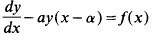
- Part of
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 80-86
- Print publication:
- June 1986
-
- Article
- Export citation
The prime number theorem via the large sieve
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 23-30
- Print publication:
- June 1986
-
- Article
- Export citation
Non-σ-finite sets for packing measure
- Part of
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 129-136
- Print publication:
- June 1986
-
- Article
- Export citation
Approximate subdifferentials and applications II
- Part of
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 111-128
- Print publication:
- June 1986
-
- Article
- Export citation
A polyhedral model for Cartan's Hypersurface in S4
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 55-61
- Print publication:
- June 1986
-
- Article
- Export citation
On the Koszul homology modules for the powers of a multiplicity system
- Part of
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 96-101
- Print publication:
- June 1986
-
- Article
- Export citation
Normal subgroups of skew linear groups
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 102-110
- Print publication:
- June 1986
-
- Article
- Export citation
Mean values of character sums
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-5
- Print publication:
- June 1986
-
- Article
- Export citation
On Waring's problem for smaller exponents. II
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 6-22
- Print publication:
- June 1986
-
- Article
- Export citation
Positive values of indefinite quadratic forms
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 164-169
- Print publication:
- June 1986
-
- Article
- Export citation
The number of polytopes, configurations and real matroids
- Part of
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 62-71
- Print publication:
- June 1986
-
- Article
- Export citation
The Akivis algebra of a homogeneous loop
- Part of
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 87-95
- Print publication:
- June 1986
-
- Article
- Export citation
Note on irregularities of distribution
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 148-163
- Print publication:
- June 1986
-
- Article
- Export citation
Some examples of Borel-inseparable pairs of coanalylic sets
- Part of
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 72-79
- Print publication:
- June 1986
-
- Article
- Export citation
Chapter 6 - Graphs and Series-Parallel Networks
-
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp 97-126
-
- Chapter
- Export citation
Contents
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp v-viii
-
- Chapter
- Export citation
ENCYCLOPEDIA OF MATHEMATICS AND ITS APPLICATIONS
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp 317-318
-
- Chapter
- Export citation
Preface
-
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp xv-xviii
-
- Chapter
- Export citation
Appendix of Matroid Cryptomorphisms
-
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp 298-312
-
- Chapter
- Export citation
List of Contributors
-
- Book:
- Theory of Matroids
- Published online:
- 05 May 2010
- Print publication:
- 03 April 1986, pp ix-x
-
- Chapter
- Export citation
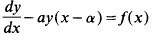
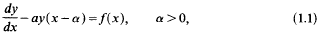
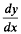 over 0 < x < α. As a result of integration, the value of
over 0 < x < α. As a result of integration, the value of 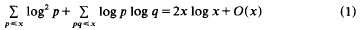
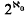 disjoint compact subsets each of non-σ-finite measure. The corresponding problem for Hausdorff measures is discussed, but not completely resolved, in Rogers' book [7]. We also show that packing measure cannot be attained by taking the Hausdorff measure with respect to a different increasing function using another metric which generates the same topology. This means that the class of pacing measures is distinct from the class of Hausdorff measures.
disjoint compact subsets each of non-σ-finite measure. The corresponding problem for Hausdorff measures is discussed, but not completely resolved, in Rogers' book [7]. We also show that packing measure cannot be attained by taking the Hausdorff measure with respect to a different increasing function using another metric which generates the same topology. This means that the class of pacing measures is distinct from the class of Hausdorff measures.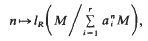
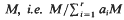 has finite length.
has finite length.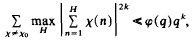
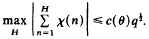
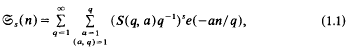
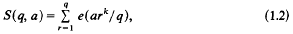
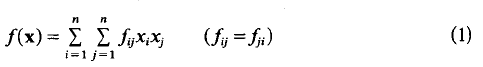
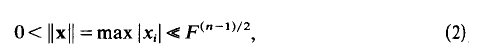
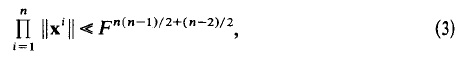
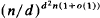 , as
, as 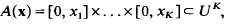
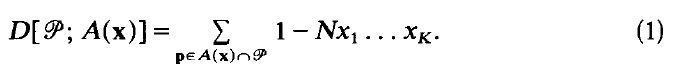
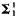 ) if it is the continuous image of a Borel set (in any space), or equivalently, the projection of a Borel set, and is
) if it is the continuous image of a Borel set (in any space), or equivalently, the projection of a Borel set, and is 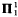 ) if it is the complement of an analytic set. The class of analytic sets is closed under countable unions and intersections, images and preimages by Borel measurable functions, and projections; it is not closed under complements, hence there is an analytic set which is not Borel.
) if it is the complement of an analytic set. The class of analytic sets is closed under countable unions and intersections, images and preimages by Borel measurable functions, and projections; it is not closed under complements, hence there is an analytic set which is not Borel.