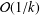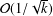Refine search
Actions for selected content:
8125 results in Fluid dynamics and solid mechanics
FEEDBACK PREDICTIVE CONTROL OF NONHOMOGENEOUS MARKOV JUMP SYSTEMS WITH NONSYMMETRIC CONSTRAINTS
-
- Journal:
- The ANZIAM Journal / Volume 56 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 18 December 2014, pp. 138-149
-
- Article
-
- You have access
- Export citation

Scaling, Self-similarity, and Intermediate Asymptotics
- Dimensional Analysis and Intermediate Asymptotics
-
- Published online:
- 18 December 2014
- Print publication:
- 12 December 1996
Copyright page
-
- Book:
- Flow in Porous Rocks
- Published online:
- 05 January 2015
- Print publication:
- 18 December 2014, pp iv-iv
-
- Chapter
- Export citation
2 - Porous rocks
-
- Book:
- Flow in Porous Rocks
- Published online:
- 05 January 2015
- Print publication:
- 18 December 2014, pp 11-27
-
- Chapter
- Export citation
11 - Geothermal power and heat storage
-
- Book:
- Flow in Porous Rocks
- Published online:
- 05 January 2015
- Print publication:
- 18 December 2014, pp 227-261
-
- Chapter
- Export citation
12 - Compressibility and gas flows
-
- Book:
- Flow in Porous Rocks
- Published online:
- 05 January 2015
- Print publication:
- 18 December 2014, pp 262-278
-
- Chapter
- Export citation
Contents
-
- Book:
- Flow in Porous Rocks
- Published online:
- 05 January 2015
- Print publication:
- 18 December 2014, pp v-viii
-
- Chapter
- Export citation
ADVENTURES IN INVARIANT THEORY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 56 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 15 December 2014, pp. 105-115
-
- Article
-
- You have access
- Export citation
SOLVING INFINITE-HORIZON OPTIMAL CONTROL PROBLEMS USING THE HAAR WAVELET COLLOCATION METHOD
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 56 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 15 December 2014, pp. 179-191
-
- Article
-
- You have access
- Export citation
LARGE INTERVAL SOLUTION OF THE EMDEN–FOWLER EQUATION USING A MODIFIED ADOMIAN DECOMPOSITION METHOD WITH AN INTEGRATING FACTOR
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 56 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 15 December 2014, pp. 192-208
-
- Article
-
- You have access
- Export citation
DISTRIBUTED PROXIMAL-GRADIENT METHOD FOR CONVEX OPTIMIZATION WITH INEQUALITY CONSTRAINTS
-
- Journal:
- The ANZIAM Journal / Volume 56 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 18 November 2014, pp. 160-178
-
- Article
-
- You have access
- Export citation

Magnetoconvection
-
- Published online:
- 05 November 2014
- Print publication:
- 30 October 2014
9 - Solar and stellar magnetic fields
-
- Book:
- Magnetoconvection
- Published online:
- 05 November 2014
- Print publication:
- 30 October 2014, pp 320-348
-
- Chapter
- Export citation
8 - Compressible magnetoconvection
-
- Book:
- Magnetoconvection
- Published online:
- 05 November 2014
- Print publication:
- 30 October 2014, pp 251-319
-
- Chapter
- Export citation
2 - Basic MHD
-
- Book:
- Magnetoconvection
- Published online:
- 05 November 2014
- Print publication:
- 30 October 2014, pp 9-37
-
- Chapter
- Export citation
Preface
-
- Book:
- Magnetoconvection
- Published online:
- 05 November 2014
- Print publication:
- 30 October 2014, pp ix-xii
-
- Chapter
- Export citation
4 - The nonlinear regime
-
- Book:
- Magnetoconvection
- Published online:
- 05 November 2014
- Print publication:
- 30 October 2014, pp 64-112
-
- Chapter
- Export citation
Appendix A - The Boussinesq and anelastic approximations
-
- Book:
- Magnetoconvection
- Published online:
- 05 November 2014
- Print publication:
- 30 October 2014, pp 349-354
-
- Chapter
- Export citation
5 - 2D Boussinesq magnetoconvection
-
- Book:
- Magnetoconvection
- Published online:
- 05 November 2014
- Print publication:
- 30 October 2014, pp 113-179
-
- Chapter
- Export citation
7 - Magnetoconvection, rotation and the dynamo
-
- Book:
- Magnetoconvection
- Published online:
- 05 November 2014
- Print publication:
- 30 October 2014, pp 215-250
-
- Chapter
- Export citation