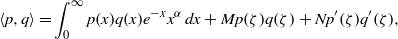Refine search
Actions for selected content:
8125 results in Fluid dynamics and solid mechanics
A TRANSFORMATION METHOD FOR SOLVING THE HAMILTON–JACOBI–BELLMAN EQUATION FOR A CONSTRAINED DYNAMIC STOCHASTIC OPTIMAL ALLOCATION PROBLEM
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 1 / July 2013
- Published online by Cambridge University Press:
- 10 October 2013, pp. 14-38
-
- Article
-
- You have access
- Export citation
ON LAGUERRE–SOBOLEV TYPE ORTHOGONAL POLYNOMIALS: ZEROS AND ELECTROSTATIC INTERPRETATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 1 / July 2013
- Published online by Cambridge University Press:
- 08 October 2013, pp. 39-54
-
- Article
-
- You have access
- Export citation

Double-Diffusive Convection
-
- Published online:
- 05 October 2013
- Print publication:
- 19 September 2013

Cavitation and Bubble Dynamics
-
- Published online:
- 05 October 2013
- Print publication:
- 14 October 2013
3 - The unbounded gradient model
-
- Book:
- Double-Diffusive Convection
- Published online:
- 05 October 2013
- Print publication:
- 19 September 2013, pp 32-57
-
- Chapter
- Export citation
Double-Diffusive Convection - Title page
-
-
- Book:
- Double-Diffusive Convection
- Published online:
- 05 October 2013
- Print publication:
- 19 September 2013, pp iii-iii
-
- Chapter
- Export citation
Double-Diffusive Convection - Half title page
-
- Book:
- Double-Diffusive Convection
- Published online:
- 05 October 2013
- Print publication:
- 19 September 2013, pp i-ii
-
- Chapter
- Export citation
Dedication
-
- Book:
- Double-Diffusive Convection
- Published online:
- 05 October 2013
- Print publication:
- 19 September 2013, pp v-vii
-
- Chapter
- Export citation
Contents
-
- Book:
- Double-Diffusive Convection
- Published online:
- 05 October 2013
- Print publication:
- 19 September 2013, pp viii-x
-
- Chapter
- Export citation
Index
-
- Book:
- Double-Diffusive Convection
- Published online:
- 05 October 2013
- Print publication:
- 19 September 2013, pp 340-342
-
- Chapter
- Export citation
7 - Thermohaline intrusions
-
- Book:
- Double-Diffusive Convection
- Published online:
- 05 October 2013
- Print publication:
- 19 September 2013, pp 108-170
-
- Chapter
- Export citation
Copyright page
-
- Book:
- Double-Diffusive Convection
- Published online:
- 05 October 2013
- Print publication:
- 19 September 2013, pp iv-iv
-
- Chapter
- Export citation
12 - Beyond oceanography
-
- Book:
- Double-Diffusive Convection
- Published online:
- 05 October 2013
- Print publication:
- 19 September 2013, pp 275-310
-
- Chapter
- Export citation
10 - Double-diffusion in active environments
-
- Book:
- Double-Diffusive Convection
- Published online:
- 05 October 2013
- Print publication:
- 19 September 2013, pp 216-247
-
- Chapter
- Export citation
2 - The linear instability problem
-
- Book:
- Double-Diffusive Convection
- Published online:
- 05 October 2013
- Print publication:
- 19 September 2013, pp 17-31
-
- Chapter
- Export citation
13 - Perspectives and challenges
-
- Book:
- Double-Diffusive Convection
- Published online:
- 05 October 2013
- Print publication:
- 19 September 2013, pp 311-315
-
- Chapter
- Export citation
5 - The bounded layer model
-
- Book:
- Double-Diffusive Convection
- Published online:
- 05 October 2013
- Print publication:
- 19 September 2013, pp 76-92
-
- Chapter
- Export citation
References
-
- Book:
- Double-Diffusive Convection
- Published online:
- 05 October 2013
- Print publication:
- 19 September 2013, pp 316-339
-
- Chapter
- Export citation
8 - Thermohaline staircases
-
- Book:
- Double-Diffusive Convection
- Published online:
- 05 October 2013
- Print publication:
- 19 September 2013, pp 171-211
-
- Chapter
- Export citation
1 - General principles
-
- Book:
- Double-Diffusive Convection
- Published online:
- 05 October 2013
- Print publication:
- 19 September 2013, pp 1-16
-
- Chapter
- Export citation