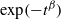Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
DETERMINATION OF JOIN REGIONS BETWEEN CARBON NANOSTRUCTURES USING VARIATIONAL CALCULUS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 04 September 2013, pp. 221-247
-
- Article
-
- You have access
- Export citation
APPROXIMATING THE KOHLRAUSCH FUNCTION BY SUMS OF EXPONENTIALS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 04 September 2013, pp. 306-323
-
- Article
-
- You have access
- Export citation
ANZ VOLUME 54 ISSUE 4 COVER AND FRONT MATTER
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 04 September 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Dedication
-
- Book:
- An Introduction to Continuum Mechanics
- Published online:
- 05 July 2013
- Print publication:
- 29 July 2013, pp v-vi
-
- Chapter
- Export citation
6 - CONSTITUTIVE EQUATIONS
-
- Book:
- An Introduction to Continuum Mechanics
- Published online:
- 05 July 2013
- Print publication:
- 29 July 2013, pp 221-264
-
- Chapter
- Export citation
1 - INTRODUCTION
-
- Book:
- An Introduction to Continuum Mechanics
- Published online:
- 05 July 2013
- Print publication:
- 29 July 2013, pp 1-8
-
- Chapter
- Export citation
Contents
-
- Book:
- An Introduction to Continuum Mechanics
- Published online:
- 05 July 2013
- Print publication:
- 29 July 2013, pp vii-xvi
-
- Chapter
- Export citation
9 - LINEARIZED VISCOELASTICITY
-
- Book:
- An Introduction to Continuum Mechanics
- Published online:
- 05 July 2013
- Print publication:
- 29 July 2013, pp 389-424
-
- Chapter
- Export citation
About the Author
-
- Book:
- An Introduction to Continuum Mechanics
- Published online:
- 05 July 2013
- Print publication:
- 29 July 2013, pp xxvii-xxviii
-
- Chapter
- Export citation
8 - FLUID MECHANICS AND HEAT TRANSFER
-
- Book:
- An Introduction to Continuum Mechanics
- Published online:
- 05 July 2013
- Print publication:
- 29 July 2013, pp 355-388
-
- Chapter
- Export citation
7 - LINEARIZED ELASTICITY
-
- Book:
- An Introduction to Continuum Mechanics
- Published online:
- 05 July 2013
- Print publication:
- 29 July 2013, pp 265-354
-
- Chapter
- Export citation
5 - CONSERVATION AND BALANCE LAWS
-
- Book:
- An Introduction to Continuum Mechanics
- Published online:
- 05 July 2013
- Print publication:
- 29 July 2013, pp 181-220
-
- Chapter
- Export citation
Preface to the Second Edition
-
- Book:
- An Introduction to Continuum Mechanics
- Published online:
- 05 July 2013
- Print publication:
- 29 July 2013, pp xxiii-xxiv
-
- Chapter
- Export citation
Answers to Selected Problems
-
- Book:
- An Introduction to Continuum Mechanics
- Published online:
- 05 July 2013
- Print publication:
- 29 July 2013, pp 429-440
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- An Introduction to Continuum Mechanics
- Published online:
- 05 July 2013
- Print publication:
- 29 July 2013, pp i-iv
-
- Chapter
- Export citation
References for Additional Reading
-
- Book:
- An Introduction to Continuum Mechanics
- Published online:
- 05 July 2013
- Print publication:
- 29 July 2013, pp 425-428
-
- Chapter
- Export citation
List of Symbols
-
- Book:
- An Introduction to Continuum Mechanics
- Published online:
- 05 July 2013
- Print publication:
- 29 July 2013, pp xvii-xxii
-
- Chapter
- Export citation
Preface to the First Edition
-
- Book:
- An Introduction to Continuum Mechanics
- Published online:
- 05 July 2013
- Print publication:
- 29 July 2013, pp xxv-xxvi
-
- Chapter
- Export citation
Index
-
- Book:
- An Introduction to Continuum Mechanics
- Published online:
- 05 July 2013
- Print publication:
- 29 July 2013, pp 441-450
-
- Chapter
- Export citation
2 - VECTORS AND TENSORS
-
- Book:
- An Introduction to Continuum Mechanics
- Published online:
- 05 July 2013
- Print publication:
- 29 July 2013, pp 9-80
-
- Chapter
- Export citation