Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Aspects of laser Lorenz dynamics
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 152-174
-
- Article
-
- You have access
- Export citation
One-dimensional pattern formation in a model of burning
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 17 February 2009, pp. 145-173
-
- Article
-
- You have access
- Export citation
On the variational stability of a class of nonlinear parabolic optimal control problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 1 / July 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 77-92
-
- Article
-
- You have access
- Export citation
Scattering of water waves by a submerged nearly circular cylinder
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 3 / January 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 372-380
-
- Article
-
- You have access
- Export citation
ANZ volume 45 issue 1 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 1 / July 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
An open-channel flow meeting a barrier and forming one or two jets
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 4 / April 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 458-472
-
- Article
-
- You have access
- Export citation
A transformation to linearity of some non-linear differential-difference equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 4 / April 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 416-419
-
- Article
-
- You have access
- Export citation
Two-point formulae of Euler type
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 221-245
-
- Article
-
- You have access
- Export citation
The properties of solutions of weakly singular integral equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 419-430
-
- Article
-
- You have access
- Export citation
Necessary conditions for a mathematical programming problem with set and cone constraints
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 3 / January 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 310-321
-
- Article
-
- You have access
- Export citation
Sinc approximation of Cauchy-type integrals over arcs
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 1 / July 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 87-97
-
- Article
-
- You have access
- Export citation
Fast diffusion with loss at infinity
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 4 / April 1996
- Published online by Cambridge University Press:
- 17 February 2009, p. 571
-
- Article
-
- You have access
- Export citation
An analytical solution for critical withdrawal of layered fluid through a line sink in a porous medium
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 271-279
-
- Article
-
- You have access
- Export citation
A tournament problem
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 3 / January 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 289-291
-
- Article
-
- You have access
- Export citation
ANZ volume 49 issue 2 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b3
-
- Article
-
- You have access
- Export citation
Numerical solitary wave interaction: the order of the inelastic effect
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 1 / July 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 95-102
-
- Article
-
- You have access
- Export citation
Equations for periodic solutions of a logistic difference equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 1 / July 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 78-94
-
- Article
-
- You have access
- Export citation
Radiating Demianski-type metrics and the Einstein-Maxwell fields
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 1 / July 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 120-126
-
- Article
-
- You have access
- Export citation
A nonlinear singular perturbation problem on a semi-infinite interval
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 17 February 2009, pp. 226-240
-
- Article
-
- You have access
- Export citation
ANZ volume 39 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 4 / April 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
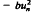 , where
, where 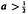 and
and 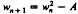 , where
, where 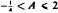 , although the equations obtained are valid for
, although the equations obtained are valid for 