Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Eigenvalues of the Laplacian for the third boundary value problem
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 1 / July 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. 79-87
-
- Article
-
- You have access
- Export citation
Extended optima and equilibria for continuous games. I. General results
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 3 / January 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 291-307
-
- Article
-
- You have access
- Export citation
On eigensolutions of the one-speed neutron transport equation in plane geometry
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. 223-230
-
- Article
-
- You have access
- Export citation
Dominated strategies in searching for evolutionary stable strategies
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 2 / October 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 214-219
-
- Article
-
- You have access
- Export citation
Transient electromagnetic response of a layered conducting medium at asymptotically late times
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 1 / July 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 1-30
-
- Article
-
- You have access
- Export citation
Eigenvalues of the Laplacian with Neumann boundary conditions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 3 / January 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 293-309
-
- Article
-
- You have access
- Export citation
Exact solution of a difference approximation to Duffing's equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 1 / July 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 64-77
-
- Article
-
- You have access
- Export citation
Nonlinearly constrained optimal control problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 4 / April 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 517-530
-
- Article
-
- You have access
- Export citation
A comparative study of simulation techniques for two dimensional data honouring specified exponential semivariograms
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 3 / January 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 249-260
-
- Article
-
- You have access
- Export citation
ANZ volume 24 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 2 / October 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Contents of Volume 43
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 4 / April 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 587-589
-
- Article
-
- You have access
- Export citation
The time fractional diffusion equation and the advection-dispersion equation
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 3 / January 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 317-330
-
- Article
-
- You have access
- Export citation
Braess's paradox and power-law nonlinearities in networks
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 1 / July 1993
- Published online by Cambridge University Press:
- 17 February 2009, pp. 1-22
-
- Article
-
- You have access
- Export citation
Fourth order nonlinear evolution equations for gravity-capillary waves in the presence of a thin thermocline in deep water
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 4 / April 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 513-524
-
- Article
-
- You have access
- Export citation
Contents of Volume 29
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 4 / April 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 501-502
-
- Article
-
- You have access
- Export citation
Groups defined on images in fluid diffusion
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 1 / July 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 101-119
-
- Article
-
- You have access
- Export citation
Poisson approximations for telecommunications networks
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 3 / January 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 348-364
-
- Article
-
- You have access
- Export citation
ANZ volume 42 issue 2 Back matter
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Cavities at atmospheric pressure behind two-dimensional bodies at an angle of attack
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 1 / July 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 103-119
-
- Article
-
- You have access
- Export citation
Gas and water cresting towards horizontal wells
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 17 February 2009, pp. 174-197
-
- Article
-
- You have access
- Export citation
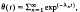 , where
, where 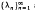 are the eigenvalues of the two-dimensional Laplacian, is studied for a variety of domains. The dependence of θ(
are the eigenvalues of the two-dimensional Laplacian, is studied for a variety of domains. The dependence of θ(