Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Selective withdrawal from stratified streams
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 1 / July 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 26-40
-
- Article
-
- You have access
- Export citation
Duality for linear multiplicative programs
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 3 / January 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 393-397
-
- Article
-
- You have access
- Export citation
Black holes and solitons of the quantized dispersionless NLS and DNLS equations
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 1 / July 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 73-81
-
- Article
-
- You have access
- Export citation
The limiting ideal theory for shear-index cohesionless granular materials
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 3 / January 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 373-392
-
- Article
-
- You have access
- Export citation
Insulating circular rugs
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 4 / April 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 359-365
-
- Article
-
- You have access
- Export citation
A method for the study of fully developed parallel flow in straight ducts of arbitrary cross section
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 211-239
-
- Article
-
- You have access
- Export citation
On the generation of water waves at an inertial surface
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 3 / January 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 366-383
-
- Article
-
- You have access
- Export citation
Sigmoidal cosine series on the interval
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 4 / April 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 451-475
-
- Article
-
- You have access
- Export citation
Second method of Lyapunov and comparison principle for impulsive differential–difference equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 4 / April 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 489-505
-
- Article
-
- You have access
- Export citation
A-topology for Minkowski space
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 1 / April 1979
- Published online by Cambridge University Press:
- 17 February 2009, pp. 53-64
-
- Article
-
- You have access
- Export citation
The dimension of attractors of nonautonomous partial differential equations
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 207-222
-
- Article
-
- You have access
- Export citation
Fast local convergence with single and multistep methods for nonlinear equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 17 February 2009, pp. 173-199
-
- Article
-
- You have access
- Export citation
Boundary value controllability and observability problems for the wave and heat equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 4 / April 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 461-479
-
- Article
-
- You have access
- Export citation
Three dimensional similarity solutions of the nonlinear diffusion equation from optimization and first integrals
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 3 / January 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 297-309
-
- Article
-
- You have access
- Export citation
The diffraction of elastic waves by small cylindrical cavities†
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 3 / January 1980
- Published online by Cambridge University Press:
- 17 February 2009, p. 384
-
- Article
-
- You have access
- Export citation
ANZ volume 26 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 4 / April 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Global strong solutions of equations of magnetohydrodynamic type
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 3 / January 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 291-306
-
- Article
-
- You have access
- Export citation
Evaluation of the acoustic impedance of a screen
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 17 February 2009, pp. 46-61
-
- Article
-
- You have access
- Export citation
Stern waves with vorticity
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 3 / January 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 321-332
-
- Article
-
- You have access
- Export citation
A closed-form analytical solution for the valuation of convertible bonds with constant dividend yield
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 4 / April 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 477-494
-
- Article
-
- You have access
- Export citation
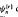 composed of a cosine function and a sigmoidal transformation γ
composed of a cosine function and a sigmoidal transformation γ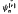 converges uniformly to
converges uniformly to 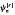 according to the value of
according to the value of 