Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
ANZ volume 37 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 1 / July 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
ANZ volume 19 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
What is a shell-crossing singularity?
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 167-179
-
- Article
-
- You have access
- Export citation
Sharp integral inequalities based on general Euler two-point formulae
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 4 / April 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 555-574
-
- Article
-
- You have access
- Export citation
Variance Minimization – Relationship between Completion-Time Variance and Waiting-Time Variance
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 1 / July 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 126-139
-
- Article
-
- You have access
- Export citation
Water waves, nonlinear Schrödinger equations and their solutions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 1 / July 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 16-43
-
- Article
-
- You have access
- Export citation
ANZ volume 48 issue 1 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 1 / July 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b3
-
- Article
-
- You have access
- Export citation
Solution of nonlinear equations and computation of multiple solutions of a simple reaction-diffusion equation
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 1 / July 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 55-64
-
- Article
-
- You have access
- Export citation
Observables in modular field thoey
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 2 / October 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. 221-248
-
- Article
-
- You have access
- Export citation
n-Dimensional first integral and similarity solutions for two-phase flow
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 3 / January 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 365-380
-
- Article
-
- You have access
- Export citation
ANZ volume 33 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Hyperelliptic parametrisation of the generalised order parameter of the N = 3 chiral Potts model
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 3 / January 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 289-307
-
- Article
-
- You have access
- Export citation
On an exact WKB approach to Ablowitz-Segur's connection problem for the second Painlevé equation
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 1 / July 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 111-119
-
- Article
-
- You have access
- Export citation
Spectral factorisation and prediction of multivariate processes with time-dependent rational spectral density matrices
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 192-210
-
- Article
-
- You have access
- Export citation
Contents of volume 47
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 4 / April 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 593-595
-
- Article
-
- You have access
- Export citation
The effect of a submerged barrier on the natural freqencies and radiation damping of a shallow basin connected to open water
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 1 / July 1980
- Published online by Cambridge University Press:
- 17 February 2009, pp. 104-128
-
- Article
-
- You have access
- Export citation
Generalized shear deformations for isotropic incompressible hyperelastic materials
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 17 February 2009, pp. 129-141
-
- Article
-
- You have access
- Export citation
Locating oscillatory orbits of the parametrically-excited pendulum
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 3 / January 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 309-319
-
- Article
-
- You have access
- Export citation
The multiplicity of steady-state solutions arising from microwave heating. I. Infinite Biot number and small penetration depth
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 1 / July 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 87-103
-
- Article
-
- You have access
- Export citation
On the uniqueness of solitary Rossby waves
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 4 / April 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. 476-485
-
- Article
-
- You have access
- Export citation
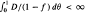 and
and 