Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
ANZ volume 34 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 3 / January 1993
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Lattice vibrations with Rayleigh dissipation
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 244-253
-
- Article
-
- You have access
- Export citation
On some noncoercive variational inequalities containing degenerate elliptic operators
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 3 / January 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 409-430
-
- Article
-
- You have access
- Export citation
Some axially symmetric zero mass meson solutions of Einstein's equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 17 February 2009, pp. 140-145
-
- Article
-
- You have access
- Export citation
On the problem of uncoupling systems of linear differential equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 4 / April 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 483-501
-
- Article
-
- You have access
- Export citation
An epidemic model for the transmission dynamics of HIV and another pathogen
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 181-193
-
- Article
-
- You have access
- Export citation
ANZ volume 44 issue 2 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b3
-
- Article
-
- You have access
- Export citation
Combustion waves
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 4 / April 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 464-476
-
- Article
-
- You have access
- Export citation
Saddle point criteria and duality in multiobjective programming via an η-approximation method
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 155-172
-
- Article
-
- You have access
- Export citation
On nonblocking multiconnection networks composed of digital switching matrices
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 188-203
-
- Article
-
- You have access
- Export citation
Singular perturbation methods for a class of initial and boundary value problems in multi-parameter classical digital control systems
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 1 / July 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 67-77
-
- Article
-
- You have access
- Export citation
Asymptotic behavior of solutions to the Stefan problem with a kinetic condition at the free boundary
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 1 / July 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 81-96
-
- Article
-
- You have access
- Export citation
An analysis of the impact of T. M. Cherry's work on asymptotic expansions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 4 / April 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 378-388
-
- Article
-
- You have access
- Export citation
Modelling the spread of grass fires
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 4 / April 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 451-466
-
- Article
-
- You have access
- Export citation
Contents
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 4 / December 1976
- Published online by Cambridge University Press:
- 17 February 2009, pp. 513-514
-
- Article
-
- You have access
- Export citation
Facility location via continuous optimization with discontinuous objective functions
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 3 / January 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. 315-325
-
- Article
-
- You have access
- Export citation
Optimal control of a chemical reactor
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 1 / July 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 61-76
-
- Article
-
- You have access
- Export citation
The molecular weight distribution problem and reptation mixing rules
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 1 / July 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 26-40
-
- Article
-
- You have access
- Export citation
ANZ volume 23 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 2 / October 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
ANZ volume 35 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
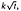 , δ
, δ