Oxygen index methods have been widely used to measure the flammability of polymeric materials and to investigate the effectiveness of fire-retardants. Using a dynamical systems framework we show how a limiting oxygen index can be identified with an appropriate bifurcation.

The effectiveness of fire-retardants in changing the limiting oxygen index is calculated by unfolding the bifurcation point with a suitable non-dimensionalised variable, which depends upon the mode of action of the additive. In order to use this procedure it is essential the model is non-dimensionalised so as to retain the variables of interest as distinct continuation parameters.

A class of mixed control-state constrained optimal control problems for elliptic partial differential equations arising, for example, in Lavrentiev-type regularized state constrained optimal control is considered. Its numerical solution is obtained via a primal-dual activeset method, which is equivalent to a class of semi-smooth Newton methods. The locally superlinear convergence of the active-set method in function space is established, and its mesh independence is proved. The paper contains a report on numerical test runs including a comparison with a short-step path-following interior-point method and a coarse-to-fine mesh sweep, that is, a nested iteration technique, for accelerating the overall solution process. Finally, convergence and regularity properties of the regularized problems with respect to a vanishing Lavrentiev parameter are considered. 2000 Mathematics subject classification: primary 65K05; secondary 90C33.

The sums

are shown to approximate J0 (z); the error terms are series in higher order Bessel functions, leading with J2M (z). Similar sums approximate J1(z). These sums may be looked on as extensions of the Jacobi expansions for cos z and sin z in series of Bessel functions. They become numerically useful for M > |z|.

This paper is devoted to the study of the solvability of certain one-and multidimensional Abel-type integral equations involving the Gauss hypergeometric function as their kernels in the space of summable functions. The multidimensional equations are considered over certain pyramidal domains and the results obtained are used to present the multidimensional pyramidal analogues of generalized fractional calculus operators and their properties.

A generalised form of the Reynolds equation for two symmetrical surfaces is derived by considering slip at the bearing surfaces. This equation is then used to study the effects of velocity-slip for the lubrication of journal bearings using half-Sommerfeld boundary conditions. Expressions for pressure and load capacity and the coefficient of friction are obtained and numerically analysed for various parameters. It is found that the load capacity decreases with slip. This is unfavourable for lubrication. The coefficient of friction decreases with a high viscous layer and increases with slip.

Following work in an earlier paper, the theory of finite deformation of elastic membranes is applied to the problem of two initially-circular semi-infinite cylindrical membranes of the same radius but of different material, joined longitudinally at a cross-section. The body is inflated by constant interior pressure and is also extended longitudinally. The exact solution found for an arbitrary material is now specialised to the orthotropic case, and the results are interpreted for forms of the strain-energy function introduced by Vaishnav and by How and Clarke in connection with the study of arteries. Also considered in this context is the similar problem where two semi-infinite cylindrical membranes of the same material are separated by a cuff of different material. Numerical solutions are obtained for various pressures and longitudinal extensions. It is shown that discontinuities in the circumferential stress at the joint can be reduced by suitable choice of certain coefficients in the expression defining the strain-energy function. The results obtained here thus solve the problem of static internal pressure loading in extended dissimilar thin orthotropic tubes, and may also be useful in the preliminary study of surgical implants in arteries.

This paper gives an approximate solution to the Wiener-Hopf integral equation for filtering fractional Riesz-Bessel motion. This is obtained by showing that the corresponding covariance operator of the integral equation is a continuous isomorphism between appropriate fractional Sobolev spaces. The proof relies on properties of the Riesz and Bessel potentials and the theory of fractional Sobolev spaces.

Sufficient conditions are given for the occurrence of various types of asymptotic behaviour in the solution of a class of n th order neutral delay differential equations. The conditions are in the form of certain inequalities amongst the constants involved in the definition of the differential equations, and specify either oscillatory behavior, or asymptotic divergence, or solutions which converge to zero.

A small gas bubble in a liquid, when driven by intense ultrasound, collapses and emits light in a process called Single-Bubble Sonoluminescence (SBSL). While the dynamics of driven bubbles are well studied, less is known of the physical conditions in the gas or whether it is necessary to include ionisation in simpler studies of bubble dynamics. In this study, a model was derived from Rayleigh-Plesset dynamics, a van der Waals equation of state and the first law of thermodynamics (including interfacial heat transfer and ionisation). Stronger model ionisation reduced the maximum collapse temperature, and altered other collapse characteristics. Chaotic parameter regions are proximal to, but not coincident with, known stable SL regions. Resonant behaviour was only markedly affected by ionisation close to these chaotic regions.

The unsteady axisymmetric withdrawal from a fluid with a free surface through a point sink is considered. Results both with and without surface tension are included and placed in context with previous work. The results indicate that there are two critical values of withdrawal rate at which the surface is drawn directly into the outlet, one after flow initiation and the other after the flow has been established. It is shown that the larger of these values corresponds to the point at which steady solutions no longer exist.

In this article we consider modified search directions in the endgame of interior point methods for linear programming. In this stage, the normal equations determining the search directions become ill-conditioned. The modified search directions are computed by solving perturbed systems in which the systems may be solved efficiently by the preconditioned conjugate gradient solver. A variation of Cholesky factorization is presented for computing a better preconditioner when the normal equations are ill-conditioned. These ideas have been implemented successfully and the numerical results show that the algorithms enhance the performance of the preconditioned conjugate gradients-based interior point methods.

Professor John Mahony, F.A.A., was a talented and unusual Australian applied mathematician (cf. Fowkes and Silberstein [6]), trained in Manchester in the early 1950s under James Lighthill and Richard Meyer. He may be best remembered today for his early work on multiple scales ([8]), for the soliton equation named after him and his collaborators Brooke Benjamin and Jerry Bona ([2]) and for the many students and colleagues he influenced positively. This note concerns certain illustrative examples listed in the three-part paper Stiff Systems of Ordinary Differential Equations by John and his then postdoc John Shepherd, published in the Journal of the Australian Math. Society (Series B) ([9]). After skimming their eighty-seven pages, it is hard to tell how thoroughly they understood the behavior of solutions to their sample problems (though these descriptions remain the most compelling parts of the papers). I can now admit that, sometime in the late 1970s, I recommended that (perhaps an early version of some of) these papers not be published in (I think) a SIAM journal. I am now glad Series B accepted them. Indeed, with regard to Mahony ([8]), Fowkes and Silberstein ([6]) reported “It is likely, in fact, that the JAMS paper was rejected by other more prestigious journals. This was often the case with John's work; partially because his material was almost always a departure from conventional wisdom, but also because John's writing could be rather formal and obscure.” The junior author of the 1981 papers now has achieved considerable mastery of the subject area, but couldn't have been expected to then take the helm from the opinionated Mahony who had initiated the study through his successful proposal to the Australian Research Council.

A humanoid robot system may be viewed as a collection of segments coupled at rotational joints which geometrically represent constrained rotational Lie groups. This allows a study of the dynamics of the motion of a humanoid robot. Several formulations are possible. In this paper, dual invariant topological structures are constructed and analyzed on the finite-dimensional manifolds associated with the humanoid motion. Both cohomology and homology structures are examined on the tangent (Lagrangian) as well as on the cotangent (Hamiltonian) bundles on the manifold of the humanoid motion configuration. represented by the toral Lie group. It is established all four topological structures give in essence the same description of humanoid dynamics. Practically this means that whichever of these approaches we use, ultimately we obtain the same mathematical results.

Some recent results on the optimal choice of quadrature rules for the finite element solution of eigenvalue problems are discussed in the light of some results of the author and J. Paine.

The paper presents some additional solutions of the diffusion equation

for the case s = 2, m = −1, a case that was left open in a previous discussion. These solutions behave in a manner that is physically acceptable as the time, t, increases and as the radial coordinate, r, tends to infinity.

In this paper we present a computational method for solving a class of time-lag optimal control problems with restricted phase coordinates.

The method of matched asymptotic expanisions is used to solve the problem of flow over a thin airfoil possessing a trailing-edge appendage, which may be of a general character, but is confined to a region of small size compated to the airfoil' chord. A feature of this asymptotic solution is effective de-coupling of the flow problems for the main airfoil and the flap. The special case of an attached flat flap set at an arbitrary angle is solved in detail.

We consider symmetry-breaking bifurcation points which arise in parameter-dependent nonlinear equations of the form f(x, λ) = 0. These types of bifurcation points are connected to pitchfork bifurcation points. A direct method is used to compute such points. Multiple shooting is used to discretise the two-point boundary-value problems to obtain a finite-dimensional problem.

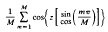
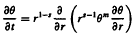
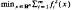A method for solving problems of the form is presented. The approach of Levenberg and Marquardt is used, except that the linear least squares subproblem arising at each iteration is not solved exactly, but only to within a certain tolerance. The method is most suited to problems in which the Jacobian matrix is sparse. Use is made of the iterative algorithm LSQR of Paige and Saunders for sparse linear least squares.

A global convergence result can be proven, and under certain conditions it can be shown that the method converges quadratically when the sum of squares at the optimal point is zero.

Numerical test results for problems of varying residual size are given.