Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
ANZ volume 47 issue 1 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 1 / July 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Partial differential equations for Eigenvalues: sensitivity and perturbation analysis
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 4 / April 1993
- Published online by Cambridge University Press:
- 17 February 2009, pp. 439-470
-
- Article
-
- You have access
- Export citation
Stability analysis from fourth order evolution equation for small but finite amplitude interfacial waves in the presence of a basic current shear
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 3 / January 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 348-365
-
- Article
-
- You have access
- Export citation
Perturbations of nonlinear autonomous oscillators
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 4 / April 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 445-468
-
- Article
-
- You have access
- Export citation
A discrete Fourier analysis of coarse mesh rebalancing and some associated iterative methods
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 2 / October 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 190-216
-
- Article
-
- You have access
- Export citation
Formation of singularities in a stratified fluid in the presence of a critical level
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 3 / January 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 316-324
-
- Article
-
- You have access
- Export citation
A nonlinear difference equation with two parameters
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 4 / April 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 430-451
-
- Article
-
- You have access
- Export citation
Diffusion and the torsion parameter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 3 / January 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 289-301
-
- Article
-
- You have access
- Export citation
Optimal diameter assignment for gas pipeline networks
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 2 / August 1979
- Published online by Cambridge University Press:
- 17 February 2009, pp. 129-144
-
- Article
-
- You have access
- Export citation
Nonlinear least squares — the Levenberg algorithm revisited*
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 3 / June 1976
- Published online by Cambridge University Press:
- 17 February 2009, pp. 343-357
-
- Article
-
- You have access
- Export citation
Uniform convergence of the collocation method for Prandtl's Integro-differential equation
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 1 / July 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 151-168
-
- Article
-
- You have access
- Export citation
A note on least-squares approximation with range constraints
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 2 / August 1979
- Published online by Cambridge University Press:
- 17 February 2009, pp. 230-242
-
- Article
-
- You have access
- Export citation
On Gerchberg's method for the Fourier inverse problem
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 1 / July 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 26-44
-
- Article
-
- You have access
- Export citation
Contents of Volume 26
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 4 / April 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 523-524
-
- Article
-
- You have access
- Export citation
A note on solitary waves with variable surface tension in water of infinite depth
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 225-235
-
- Article
-
- You have access
- Export citation
A mathematical model for the process of gas exchange in lung capillaries using nth order one-step kinetics of oxygen uptake by haemoglobin
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 2 / October 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 203-213
-
- Article
-
- You have access
- Export citation
Local transformations between some nonlinear diffusion equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 3 / January 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 321-349
-
- Article
-
- You have access
- Export citation
On the approximation order from certain multivariate spline spaces
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 233-246
-
- Article
-
- You have access
- Export citation
A note on withdrawal through a point sink in fluid of finite depth
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 3 / January 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 406-416
-
- Article
-
- You have access
- Export citation
Generalisation of a corrected Simpson's formula
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 3 / January 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 367-385
-
- Article
-
- You have access
- Export citation
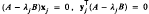 . Again, redifferentiation and combination yields slightly more complicated partial differential equations for the generalised eigenvalues. When the matrices depend on a few parameters θ
. Again, redifferentiation and combination yields slightly more complicated partial differential equations for the generalised eigenvalues. When the matrices depend on a few parameters θ