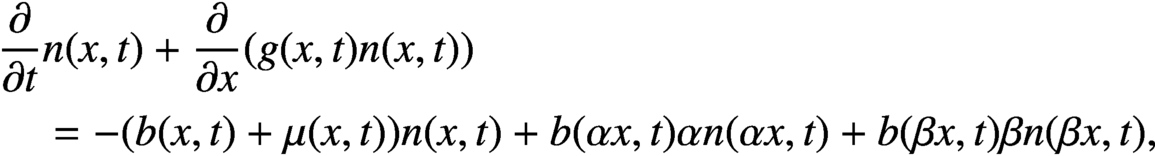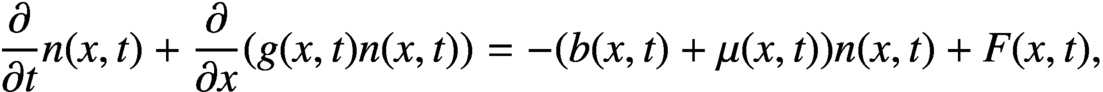Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
STOCHASTIC MODEL PREDICTIVE CONTROL FOR SPACECRAFT RENDEZVOUS AND DOCKING VIA A DISTRIBUTIONALLY ROBUST OPTIMIZATION APPROACH
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 19 April 2021, pp. 39-57
-
- Article
- Export citation

Modern Impact and Penetration Mechanics
-
- Published online:
- 01 April 2021
- Print publication:
- 22 April 2021
ESTIMATES FOR APPROXIMATE SOLUTIONS TO A FUNCTIONAL DIFFERENTIAL EQUATION MODEL OF CELL DIVISION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 12 March 2021, pp. 469-488
-
- Article
-
- You have access
- Export citation

Ocean Mixing
-
- Published online:
- 10 March 2021
- Print publication:
- 04 February 2021
ON EXISTENCE AND UNIQUENESS OF SOLUTIONS TO A PANTOGRAPH TYPE EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 03 March 2021, pp. 489-512
-
- Article
-
- You have access
- Export citation
ASYMPTOTIC ANALYSIS FOR THE MEAN FIRST PASSAGE TIME IN FINITE OR SPATIALLY PERIODIC 2D DOMAINS WITH A CLUSTER OF SMALL TRAPS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 01 March 2021, pp. 1-22
-
- Article
- Export citation
1 - Introduction
-
- Book:
- Advanced Mechanics of Solids
- Published online:
- 08 October 2021
- Print publication:
- 18 February 2021, pp 1-27
-
- Chapter
- Export citation
12 - Combined Deformations
-
- Book:
- Advanced Mechanics of Solids
- Published online:
- 08 October 2021
- Print publication:
- 18 February 2021, pp 475-495
-
- Chapter
- Export citation
7 - Analytical Solutions
-
- Book:
- Advanced Mechanics of Solids
- Published online:
- 08 October 2021
- Print publication:
- 18 February 2021, pp 180-223
-
- Chapter
- Export citation
Appendix A - Cross-Section Properties
-
- Book:
- Advanced Mechanics of Solids
- Published online:
- 08 October 2021
- Print publication:
- 18 February 2021, pp 527-536
-
- Chapter
- Export citation
Appendices
-
- Book:
- Advanced Mechanics of Solids
- Published online:
- 08 October 2021
- Print publication:
- 18 February 2021, pp 527-564
-
- Chapter
- Export citation
Contents
-
- Book:
- Advanced Mechanics of Solids
- Published online:
- 08 October 2021
- Print publication:
- 18 February 2021, pp v-x
-
- Chapter
- Export citation
4 - Strain
-
- Book:
- Advanced Mechanics of Solids
- Published online:
- 08 October 2021
- Print publication:
- 18 February 2021, pp 88-118
-
- Chapter
- Export citation
8 - Work–Energy Concepts
-
- Book:
- Advanced Mechanics of Solids
- Published online:
- 08 October 2021
- Print publication:
- 18 February 2021, pp 224-275
-
- Chapter
- Export citation
13 - Material Failure and Stability
-
- Book:
- Advanced Mechanics of Solids
- Published online:
- 08 October 2021
- Print publication:
- 18 February 2021, pp 496-526
-
- Chapter
- Export citation
Appendix C - The Sectorial Area Function
-
- Book:
- Advanced Mechanics of Solids
- Published online:
- 08 October 2021
- Print publication:
- 18 February 2021, pp 540-556
-
- Chapter
- Export citation
2 - Stress
-
- Book:
- Advanced Mechanics of Solids
- Published online:
- 08 October 2021
- Print publication:
- 18 February 2021, pp 28-68
-
- Chapter
- Export citation
3 - Equilibrium
-
- Book:
- Advanced Mechanics of Solids
- Published online:
- 08 October 2021
- Print publication:
- 18 February 2021, pp 69-87
-
- Chapter
- Export citation
Preface
-
- Book:
- Advanced Mechanics of Solids
- Published online:
- 08 October 2021
- Print publication:
- 18 February 2021, pp xi-xiv
-
- Chapter
- Export citation
Index
-
- Book:
- Advanced Mechanics of Solids
- Published online:
- 08 October 2021
- Print publication:
- 18 February 2021, pp 565-566
-
- Chapter
- Export citation