Refine search
Actions for selected content:
6994 results in Mathematical modeling and methods
Quasistationarity of continuous-time Markov chains with positive drift
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 4 / April 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 423-441
-
- Article
-
- You have access
- Export citation
Analysis of cell population PDE models with general maturation rates
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 3 / January 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 359-374
-
- Article
-
- You have access
- Export citation
ANZ volume 29 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 1 / July 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Numerical integration on the sphere
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 3 / January 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 332-347
-
- Article
-
- You have access
- Export citation
Inf-sup conditions for finite-difference approximations of the stokes equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 1 / July 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 121-134
-
- Article
-
- You have access
- Export citation
ANZ volume 30 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 3 / January 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Force distribution along a slender body straddling an interface
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 3 / January 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 295-315
-
- Article
-
- You have access
- Export citation
Contents of Volume 44
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 4 / April 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 635-638
-
- Article
-
- You have access
- Export citation
Global stability and persistence in diffusive food chains
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 247-268
-
- Article
-
- You have access
- Export citation
Homotopy continuation method for the numerical solutions of generalised symmetric eigenvalue problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 4 / April 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 437-456
-
- Article
-
- You have access
- Export citation
Some Bianchi type VI0 viscous fluid cosmological models
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 1 / July 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 77-84
-
- Article
-
- You have access
- Export citation
A note on the small-time development of the solution to a coupled, nonlinear, singular reaction-diffusion system
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 4 / April 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 581-591
-
- Article
-
- You have access
- Export citation
A note on the convergence of Halley's method for solving operator equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 1 / July 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 16-25
-
- Article
-
- You have access
- Export citation
Reduction of second order linear dynamical systems, with large dissipation, by state variable transformations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. 207-222
-
- Article
-
- You have access
- Export citation
An affine scaling interior point backtracking algorithm for nonlinear constrained optimisation
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 1 / July 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 45-66
-
- Article
-
- You have access
- Export citation
Wavelet and discrete cosine transforms for inserting information into BMP images
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 1 / July 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 23-35
-
- Article
-
- You have access
- Export citation
Sparse matrix factorizations of transfer matrices
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 4 / April 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. 462-475
-
- Article
-
- You have access
- Export citation
Bilinear and bilateral generating functions of generalized polynomials
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 257-270
-
- Article
-
- You have access
- Export citation
Poisson approximations for telecommunications networks
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 1 / July 1994
- Published online by Cambridge University Press:
- 17 February 2009, p. 132
-
- Article
-
- You have access
- Export citation
A cusp-like free-surface flow due to a submerged source or sink
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 4 / April 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 443-450
-
- Article
-
- You have access
- Export citation
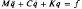 are transformed by linear state variable transformations
are transformed by linear state variable transformations 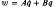 , where
, where