This paper gives a necessary and sufficient condition for a Kuhn-Tucker point of a non-smooth vector optimisation problem subject to inequality and equality constraints to be an efficient solution. The main tool we use is an alternative theorem which is quite different to a corresponding result by Xu.

We study the numerical solution of an initial-boundary value problem for a Volterra type integro-differential equation, in which the integral operator is a convolution product of a positive-definite kernel and an elliptic partial-differential operator. The equation is discretised in space by the Galerkin finite-element method and in time by finite differences in combination with various quadrature rules which preserve the positive character of the memory term. Special attention is paid to the case of a weakly singular kernel. Error estimates are derived and numerical experiments reported.

We consider a programming problem in which the objective function is the sum of a differentiable function and the p norm of Sx, where S is a matrix and p > 1. The constraints are inequality constraints defined by differentiable functions. With the aid of a recent transposition theorem of Schechter we get a duality theorem and also a converse duality theorem for this problem. This result generalizes a result of Mond in which the objective function contains the square root of a positive semi-definite quadratic function.

A new type of first baroclinic mode wave which propagates on an anti-cyclonic vorticity field in identified. It is of the vorticity class of waves which contains Rossby waves amongst others. This anti-cyclonic shear wave is produced by pressure variations distorting the vertical stratification in such a manner that the associated vortex stretching generates the velocity variation required for Bernoulli compatibility with the initial pressure variation. The wave travels at a speed characteristic of particles within the undisturbed shear flow and is a low frequency and low wavenumber wave, In the present study this wave is considered in the presence of a wark anti-cyclonic shear.

Existence criteria are presented for nonlinear singular initial and boundary value problems. In particular our theory includes a problem arising in the theory of pseudoplastic fluids.

The heart of the Lanczos algorithm is the systematic generation of orthonormal bases of invariant subspaces of a perturbed matrix. The perturbations involved are special since they are always rank-1 and are the smallest possible in certain senses. These minimal perturbation properties are extended here to more general cases.

Rank-1 perturbations are also shown to be closely connected to inverse iteration, and thus provide a novel explanation of the global convergence phenomenon of Rayleigh quotient iteration.

Finally, we show that the restriction to a Krylov subspace of a matrix differs from the restriction of its inverse by a rank-1 matrix.

The effects on adsorption of the geometry of the solid may be studied through calculations based on a (distance)−ε (ε> 3) intermolecular potential. This paper establishes the result that the potential due to an infinitely long polygonal homogeneous solid prism, at position r in the plane of its right section, is – . Here ρi = ∣ r − ri ∣, where the ri are the position vectors of the n vertices of the polygon, and θij are the angles r − ri makes with the two sides of the polygon which meet at vertex ri. The g's are exact functions of θij. They are, in general, integrals of associated Legendre functions, but they are elementary for ε an even integer. A similar result holds for the potential within an infinitely long polygonal prismatic cavity. The analysis involves a systematic superposition schema and the concept of a supplementary potential with datum within the solid at infinity. The cases ε = 6 and ε = 4 are treated in detail and illustrative solutions given for the following configurations: semi-infinite laminae, deep rectangular cracks, square prisms, square prismatic cavities and regular n-gonal prismatic cavities.

The authors derive a general theorem on partly bilateral and partly unilateral generating functions involving multiple series with essentially arbitrary coefficients. By appropriately specialising these coefficients, a number of (known or new) results are shown to follow as applications of the theorem.

This paper gives explicit, applicable bounds for solutions of a wide class of third-order difference equations with nonconstant coefficients. The techniques used are readily adaptable for higher-order equations. The results extend recent work of the authors for second-order equations.

This paper studies a system proposed by K. Gopalsamy and P. X. Weng to model a population growth with feedback control and time delays. Sufficient conditions are established under which the positive equilibrium of the system is globally attracting. The conjecture proposed by Gopalsamy and Weng is here confirmed and improved.

A three-dimensional barotropic and baroclinic model is developed to simulate currents and temperature changes induced by tropical cyclones traversing the continental shelf and slope region of the Australian North West Shelf. The model is based on a layered, explicit, finite difference formulation using the nonlinear primitive equations with an embedded entrainment scheme; a mixed-surface-layer interface is defined, which is allowed to shift from one interface to another, depending on the strength of a storm. The model has been tested by simulating the currents and temperature changes induced by tropical cyclones Orson and Ian. The modelled currents and temperatures agreed well with the available measured records except near the seabed. It has been found that the pre-storm currents have very little influence on the peak of the storm-induced currents and the currents in the wake of a tropical cyclone. The model contained no coefficients which must be calibrated for a particular application and clearly illustrated the importance of the baroclinic effects on the storm-induced response over the North West Shelf of Australia.

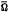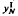Given a Fredhoim integral equation of the second kind, which is defined over a certain region ⊆ R2, we define and 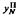, two different numerical approximations to its solution, using the collocation and iterated collocation methods respectively. We describe without proof some known results concerning the general convergence properties of and when the kernel and solution of the integral equation are smooth. Then, we prove rigorously order of convergence estimates for and which are applicable in the practically siginificant case when is a rectangle, and the kernel of the integral equation is weakly singular. These estimates are illustrated by the numerical solution of a two dimensional weakly singular equation which arises in electrical engineering.

We describe a C0-collocation-like method for solving two-dimensional elliptic Dirichlet problems on rectangular regions, using tensor products of continuous piecewise polynomials. Nodes of the Lobatto quadrature formula are taken as the points of collocation. We show that the method is stable and convergent with order hr(r ≥ 1) in the H1–norm and hr+1(r ≥ 2) in the L2–norm, if the collocation solution js a piecewise polynomial of degree not greater than r with respect to each variable. The method has an advantage over the Galerkin procedure for the same space in that no integrals need be evaluated or approximated.

Computing the generalised gradient directly using its standard definition can involve forming the convex hull of a very large number of vectors. Here an alternative concise parametrization is developed for the generalised gradient of the signed rank regression family of objective functions, a class of piecewise linear functions which includes both convex and nonconvex members. The approach uses the geometry of the epigraph explicitly and this suggests extensions to more general functions. A nondegeneracy condition is assumed which is natural in optimization problems.

Random transition probability matrices with stationary independent factors define “white noise” environment processes for Markov chains. Two examples are considered in detail. Such environment processes can be used to construct several Markov chains which are dependent, have the same transition probabilities and are jointly a Markov chain. Transition rates for such processes are evaluated. These results have application to the study of animal movements.