Refine search
Actions for selected content:
6994 results in Mathematical modeling and methods
The effect of an enclosed air cavity on a rectangular drum
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 3 / January 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 343-349
-
- Article
-
- You have access
- Export citation
Continuous-time quadratic cost flow problems with applications to water distribution networks
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 4 / April 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 530-548
-
- Article
-
- You have access
- Export citation
ANZ volume 42 issue 2 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Some boundary-value problems for nonlinear (N) diffusion and pseudo-plastic flow
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 3 / January 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 255-268
-
- Article
-
- You have access
- Export citation
On the solution of a structured nonlinear programme
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 17 February 2009, pp. 242-248
-
- Article
-
- You have access
- Export citation
On hearing the shape of an arbitrary doubly-connected region in R2
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 4 / April 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. 472-483
-
- Article
-
- You have access
- Export citation
Discrete Liapunov functions with Δ2V>0
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 3 / June 1978
- Published online by Cambridge University Press:
- 17 February 2009, pp. 280-284
-
- Article
-
- You have access
- Export citation
A formal comparison of methods proposed for the numerical solution of first kind integral equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 488-500
-
- Article
-
- You have access
- Export citation
ANZ volume 32 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 4 / April 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
On duality for convex minimization with nested maxima
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 4 / April 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 517-522
-
- Article
-
- You have access
- Export citation
Existence theory for games of pricing and technology
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 4 / April 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 575-585
-
- Article
-
- You have access
- Export citation
ANZ volume 45 issue 3 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 3 / January 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b3
-
- Article
-
- You have access
- Export citation
The numerical solution of stochastic differential equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 17 February 2009, pp. 8-12
-
- Article
-
- You have access
- Export citation
ANZ volume 31 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 4 / April 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
NMR shim coil design utilising a rapid spherical harmonic calculation method
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 3 / January 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 375-386
-
- Article
-
- You have access
- Export citation
ANZ volume 19 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Some asymptotic spectral formulae for the eigenvalues of the Laplacian
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 2 / October 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 220-229
-
- Article
-
- You have access
- Export citation
ANZ volume 49 issue 2 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
On the dynamics of a family of third-order iterative functions
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 3 / January 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. 343-359
-
- Article
-
- You have access
- Export citation
Some remarks on a Neumann boundary value problem arising in fluid dynamics
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 3 / January 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 327-332
-
- Article
-
- You have access
- Export citation
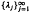 for the two-dimensional Laplacian using the asymptotic expansion of the spectral function
for the two-dimensional Laplacian using the asymptotic expansion of the spectral function 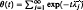 for small positive
for small positive 