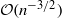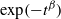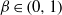Refine search
Actions for selected content:
6997 results in Mathematical modeling and methods
Stabilized Galerkin methods for magneticadvection
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 6 / November 2013
- Published online by Cambridge University Press:
- 07 October 2013, pp. 1713-1732
- Print publication:
- November 2013
-
- Article
- Export citation
Automatic simplification of Darcy’s equations with pressuredependent permeability
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 6 / November 2013
- Published online by Cambridge University Press:
- 07 October 2013, pp. 1797-1820
- Print publication:
- November 2013
-
- Article
- Export citation
A Galerkin strategy with Proper Orthogonal Decomposition forparameter-dependent problems – Analysis, assessments and applications to parameterestimation
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 6 / November 2013
- Published online by Cambridge University Press:
- 07 October 2013, pp. 1821-1843
- Print publication:
- November 2013
-
- Article
- Export citation
Eigenvalues of polyharmonic operators on variabledomains
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 19 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 06 September 2013, pp. 1225-1235
- Print publication:
- October 2013
-
- Article
- Export citation

Parameterization Schemes
- Keys to Understanding Numerical Weather Prediction Models
-
- Published online:
- 05 September 2013
- Print publication:
- 03 May 2007
A EUROPEAN OPTION GENERAL FIRST-ORDER ERROR FORMULA
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 04 September 2013, pp. 248-272
-
- Article
-
- You have access
- Export citation
ANZ VOLUME 54 ISSUE 4 COVER AND BACK MATTER
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 04 September 2013, pp. b1-b7
-
- Article
-
- You have access
- Export citation
DETERMINATION OF JOIN REGIONS BETWEEN CARBON NANOSTRUCTURES USING VARIATIONAL CALCULUS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 04 September 2013, pp. 221-247
-
- Article
-
- You have access
- Export citation
APPROXIMATING THE KOHLRAUSCH FUNCTION BY SUMS OF EXPONENTIALS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 04 September 2013, pp. 306-323
-
- Article
-
- You have access
- Export citation
ANZ VOLUME 54 ISSUE 4 COVER AND FRONT MATTER
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 04 September 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Dimension reduction for −Δ1
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 03 September 2013, pp. 42-77
- Print publication:
- January 2014
-
- Article
- Export citation
Optimal uncertainty quantification for legacy data observationsof Lipschitz functions
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 6 / November 2013
- Published online by Cambridge University Press:
- 30 August 2013, pp. 1657-1689
- Print publication:
- November 2013
-
- Article
- Export citation
Shape optimization problems for metric graphs
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 29 August 2013, pp. 1-22
- Print publication:
- January 2014
-
- Article
- Export citation
Controllability of Schrödinger equation with a nonlocalterm
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 29 August 2013, pp. 23-41
- Print publication:
- January 2014
-
- Article
- Export citation
Nash equilibrium payoffs for stochastic differential games withreflection
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 19 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 27 August 2013, pp. 1189-1208
- Print publication:
- October 2013
-
- Article
- Export citation
On the cost of null-control of an artificialadvection-diffusion problem
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 19 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 27 August 2013, pp. 1209-1224
- Print publication:
- October 2013
-
- Article
- Export citation
Two shallow-water type models for viscoelastic flows fromkinetic theory for polymers solutions
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 6 / November 2013
- Published online by Cambridge University Press:
- 26 August 2013, pp. 1627-1655
- Print publication:
- November 2013
-
- Article
- Export citation
Error estimates for the Coupled Cluster method∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 6 / November 2013
- Published online by Cambridge University Press:
- 26 August 2013, pp. 1553-1582
- Print publication:
- November 2013
-
- Article
- Export citation
Derivation of Langevin dynamics in a nonzero background flowfield
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 6 / November 2013
- Published online by Cambridge University Press:
- 20 August 2013, pp. 1583-1626
- Print publication:
- November 2013
-
- Article
- Export citation
First order second moment analysis for stochastic interfaceproblems based on low-rank approximation∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 5 / September 2013
- Published online by Cambridge University Press:
- 14 August 2013, pp. 1533-1552
- Print publication:
- September 2013
-
- Article
- Export citation