We study simple Lie algebras generated by extremal elements, over arbitrary fields of arbitrary characteristic. We show the following: (1) If the extremal geometry contains lines, then the Lie algebra admits a  $5 \times 5$-grading that can be parametrized by a cubic norm structure; (2) If there exists a field extension of degree at most
$5 \times 5$-grading that can be parametrized by a cubic norm structure; (2) If there exists a field extension of degree at most 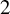 $2$ such that the extremal geometry over that field extension contains lines, and in addition, there exist symplectic pairs of extremal elements, then the Lie algebra admits a
$2$ such that the extremal geometry over that field extension contains lines, and in addition, there exist symplectic pairs of extremal elements, then the Lie algebra admits a  $5 \times 5$-grading that can be parametrized by a quadrangular algebra.
$5 \times 5$-grading that can be parametrized by a quadrangular algebra.
One of our key tools is a new definition of exponential maps that makes sense even over fields of characteristic 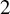 $2$ and
$2$ and 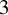 $3$, which ought to be interesting in its own right.
$3$, which ought to be interesting in its own right.
Not only was Jacques Tits a constant source of inspiration through his work, he also had a direct personal influence, notably through his threat to speak evil of our work if it did not include the characteristic 2 case.
—The Book of Involutions [KMRT98, p. xv]
 $\mathbf {5 \times 5}$-graded Lie algebras, cubic norm structures and quadrangular algebras
$\mathbf {5 \times 5}$-graded Lie algebras, cubic norm structures and quadrangular algebras
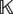 ${\mathbb{K}}$)
${\mathbb{K}}$)