Refine listing
Actions for selected content:
1959 results in 20xxx
A congruence-free inverse semigroup associated with a pair of infinite cardinals
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 3 / October 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 337-342
- Print publication:
- October 1981
-
- Article
-
- You have access
- Export citation
Growth sequences of finite groups V
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 3 / October 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 374-375
- Print publication:
- October 1981
-
- Article
-
- You have access
- Export citation
On generalizations of projectivity for modules over Dedekind domains
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 2 / August 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 207-216
- Print publication:
- August 1981
-
- Article
-
- You have access
- Export citation
A class of ideals of the centre of a group ring
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 2 / August 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 146-151
- Print publication:
- August 1981
-
- Article
-
- You have access
- Export citation
The laws of some metabelian varieties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 469-472
- Print publication:
- April 1981
-
- Article
-
- You have access
- Export citation
Isomorphisms between semigroups of isotone maps
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 453-460
- Print publication:
- April 1981
-
- Article
-
- You have access
- Export citation
A characterization of finite p-soluble groups of p-length one by commutator identities
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 3 / February 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-263
- Print publication:
- February 1981
-
- Article
-
- You have access
- Export citation
Commutative semigroup varieties with the amalgamation property
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 3 / February 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 278-283
- Print publication:
- February 1981
-
- Article
-
- You have access
- Export citation
Inverse semigroups determined by their lattices of inverse subsemigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 3 / February 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 321-346
- Print publication:
- February 1981
-
- Article
-
- You have access
- Export citation
On Fitting classes that are Schunck classes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 3 / February 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 381-384
- Print publication:
- February 1981
-
- Article
-
- You have access
- Export citation
Ideals of free inverse semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 2 / December 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 157-167
- Print publication:
- December 1980
-
- Article
-
- You have access
- Export citation
Characterization of a family of simple groups by their character table, II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 2 / December 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 168-170
- Print publication:
- December 1980
-
- Article
-
- You have access
- Export citation
Completely semisimple ring semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 2 / December 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 150-156
- Print publication:
- December 1980
-
- Article
-
- You have access
- Export citation
Some cancellation theorems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 1 / September 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 87-97
- Print publication:
- September 1980
-
- Article
-
- You have access
- Export citation
Orthodox semirings and rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 1 / September 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 50-54
- Print publication:
- September 1980
-
- Article
-
- You have access
- Export citation
A generalization of the Hall semigroup of a band
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 1 / September 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 65-72
- Print publication:
- September 1980
-
- Article
-
- You have access
- Export citation
Coextensions of pseudo-Inverse semigroups by rectangular bands
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 1 / September 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 73-86
- Print publication:
- September 1980
-
- Article
-
- You have access
- Export citation
Regular semigroups, fundamental semigroups and groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 29 / Issue 4 / June 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 475-503
- Print publication:
- June 1980
-
- Article
-
- You have access
- Export citation
On some properties of group rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 29 / Issue 4 / June 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-392
- Print publication:
- June 1980
-
- Article
-
- You have access
- Export citation
Congruences contained in an equivalence on a semigroup
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 29 / Issue 2 / March 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 162-176
- Print publication:
- March 1980
-
- Article
-
- You have access
- Export citation
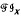 is determined by its lattice
is determined by its lattice 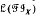 of inverse subsemigroups, in the sense that for any inverse semigroup
of inverse subsemigroups, in the sense that for any inverse semigroup 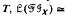
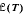 implies
implies 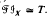 . (In fact, the lattice isomorphism is induced by an isomorphism of
. (In fact, the lattice isomorphism is induced by an isomorphism of 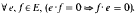 (ii) (
(ii) (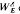 of the Hall semigroup
of the Hall semigroup 