Refine listing
Actions for selected content:
1959 results in 20xxx
Abundant Rees matrix semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 1 / February 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 132-142
- Print publication:
- February 1987
-
- Article
-
- You have access
- Export citation
On the number of p-blocks of a p-soluble group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 339-342
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
A class of finite groups having nilpotent injectors
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 361-365
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Products of locally finite groups with min-p
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 352-360
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Representations of minimally almost periodic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 366-375
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
On the number of normal subgroups of an uncountable group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 343-351
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
2-groups with every automorphism central
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 233-236
- Print publication:
- October 1986
-
- Article
-
- You have access
- Export citation
A family of simple groups associated with the Satake diagrams
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 1 / August 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 13-43
- Print publication:
- August 1986
-
- Article
-
- You have access
- Export citation
Free products of topological groups with a closed subgroup amalgamated
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 3 / June 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 414-420
- Print publication:
- June 1986
-
- Article
-
- You have access
- Export citation
Monogenic inverse semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 3 / June 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 321-342
- Print publication:
- June 1986
-
- Article
-
- You have access
- Export citation
Automorphism orbits of finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 2 / April 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 253-260
- Print publication:
- April 1986
-
- Article
-
- You have access
- Export citation
Rings satisfying certain conditions either on subsemigroups or on endomorphisms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 2 / April 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 194-202
- Print publication:
- April 1986
-
- Article
-
- You have access
- Export citation
Special series of unitary representations of groups acting on homogeneous trees
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 1 / February 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 83-88
- Print publication:
- February 1986
-
- Article
-
- You have access
- Export citation
A note on generalised wreath product groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 3 / December 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 415-420
- Print publication:
- December 1985
-
- Article
-
- You have access
- Export citation
Holomorphically parameterized families of subgroups of sl(2, ℂ)
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 248-264
- Print publication:
- December 1985
-
- Article
- Export citation
Notes on congruences on regular semigroups.I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 146-158
- Print publication:
- October 1985
-
- Article
-
- You have access
- Export citation
Semigroups of constant maps
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 241-252
- Print publication:
- October 1985
-
- Article
-
- You have access
- Export citation
A homotopy type of a p–group with cyclic centre
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 1 / August 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 94-100
- Print publication:
- August 1985
-
- Article
-
- You have access
- Export citation
Automorphisms of nilpotent groups of class two with small rank
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 1 / August 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 121-131
- Print publication:
- August 1985
-
- Article
-
- You have access
- Export citation
Multipliers of Banach valued function spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 1 / August 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 51-62
- Print publication:
- August 1985
-
- Article
-
- You have access
- Export citation
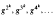 for some positive integer
for some positive integer 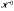 be the space of functions on the Poission boundary ω, of zero mean on ω. When
be the space of functions on the Poission boundary ω, of zero mean on ω. When 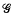 be a finitely generated subgroup of SL (2, ℱ), where ℱ is the ring; of holomorphic functions on the open unit disc Δ. For each point
be a finitely generated subgroup of SL (2, ℱ), where ℱ is the ring; of holomorphic functions on the open unit disc Δ. For each point