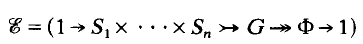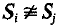Refine listing
Actions for selected content:
1959 results in 20xxx
Chief Series and Right Regular Representations of Finite p-Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 2 / April 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 225-232
- Print publication:
- April 1988
-
- Article
-
- You have access
- Export citation
On Normal Subgroups of Products of Nilpotent Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 2 / April 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 275-286
- Print publication:
- April 1988
-
- Article
-
- You have access
- Export citation
Some subgroups of the Thompson group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 1 / February 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 17-32
- Print publication:
- February 1988
-
- Article
-
- You have access
- Export citation
The odd-local subgroups of the Monster
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 1 / February 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-16
- Print publication:
- February 1988
-
- Article
-
- You have access
- Export citation
Enumerating subgroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 2 / October 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 220-223
- Print publication:
- October 1987
-
- Article
-
- You have access
- Export citation
Growth sequences of finite semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 1 / August 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 16-20
- Print publication:
- August 1987
-
- Article
-
- You have access
- Export citation
Finite semigroups with commuting idempotents
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 1 / August 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 81-90
- Print publication:
- August 1987
-
- Article
-
- You have access
- Export citation
The kernel of integral cup product
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 1 / August 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 10-15
- Print publication:
- August 1987
-
- Article
-
- You have access
- Export citation
Modular inverse semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 1 / August 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 47-63
- Print publication:
- August 1987
-
- Article
-
- You have access
- Export citation
Continuous nilpotents on topological spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 1 / August 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 127-136
- Print publication:
- August 1987
-
- Article
-
- You have access
- Export citation
Congruences and Green's relations on eventually regular semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 1 / August 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 64-69
- Print publication:
- August 1987
-
- Article
-
- You have access
- Export citation
A Construction for Fitting-Schunck classes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 1 / August 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 91-94
- Print publication:
- August 1987
-
- Article
-
- You have access
- Export citation
Automorphism groups of sandwich semigroups
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 1 / June 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 19-28
- Print publication:
- June 1987
-
- Article
- Export citation
On surface Bieberbach groups
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 1 / June 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 82-85
- Print publication:
- June 1987
-
- Article
- Export citation
Endomorphism rings of Butler groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 3 / June 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 322-329
- Print publication:
- June 1987
-
- Article
-
- You have access
- Export citation
Subnormal subgroups in direct products of groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 2 / April 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 147-172
- Print publication:
- April 1987
-
- Article
-
- You have access
- Export citation
Mal'cev products of varieties of completely regular semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 2 / April 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 227-246
- Print publication:
- April 1987
-
- Article
-
- You have access
- Export citation
CLT groups and wreath products
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 2 / April 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-195
- Print publication:
- April 1987
-
- Article
-
- You have access
- Export citation
Semidirect product groups with Abelian automorphism groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 1 / February 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 84-91
- Print publication:
- February 1987
-
- Article
-
- You have access
- Export citation
Subnormal subgroups and formation projectors
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 1 / February 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 31-47
- Print publication:
- February 1987
-
- Article
-
- You have access
- Export citation