Refine listing
Actions for selected content:
1959 results in 20xxx
Hereditary radicals and bands of associative rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 1 / August 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 62-72
- Print publication:
- August 1991
-
- Article
-
- You have access
- Export citation
Completely right pure monoids: the general case
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 1 / June 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 77-88
- Print publication:
- June 1991
-
- Article
- Export citation
Abelian groups with small cotorsion images
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 243-247
- Print publication:
- April 1991
-
- Article
-
- You have access
- Export citation
Integral and p-modular semisimple deformations for p-solvable groups of finite representation type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 213-232
- Print publication:
- April 1991
-
- Article
-
- You have access
- Export citation
Kronecker classes of field extensions of small degree
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-315
- Print publication:
- April 1991
-
- Article
-
- You have access
- Export citation
Elementary amenable groups and 4-manifolds with Euler characteristic 0
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 1 / February 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 160-170
- Print publication:
- February 1991
-
- Article
-
- You have access
- Export citation
Groups with Černikov conjugacy classes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 1 / February 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-14
- Print publication:
- February 1991
-
- Article
-
- You have access
- Export citation
Classification of 4- and 5-arc-transitive cubic graphs of small girth
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 1 / February 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 138-149
- Print publication:
- February 1991
-
- Article
-
- You have access
- Export citation
Cup products and group extensions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 1 / February 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 108-115
- Print publication:
- February 1991
-
- Article
-
- You have access
- Export citation
Static modules and non-normal Clifford theory
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 3 / December 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 347-353
- Print publication:
- December 1990
-
- Article
-
- You have access
- Export citation
On tensor induction of group representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 3 / December 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 486-501
- Print publication:
- December 1990
-
- Article
-
- You have access
- Export citation
Lie rings of groups of prime exponent
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 3 / December 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 386-398
- Print publication:
- December 1990
-
- Article
-
- You have access
- Export citation
Stably free resolutions of lattices over finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 3 / December 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 364-385
- Print publication:
- December 1990
-
- Article
-
- You have access
- Export citation
The Szendrei expansion of a semigroup
- Part of
-
- Journal:
- Mathematika / Volume 37 / Issue 2 / December 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 251-260
- Print publication:
- December 1990
-
- Article
- Export citation
Centralizing properties in simple locally finite groups and large finite classical groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 3 / December 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 502-513
- Print publication:
- December 1990
-
- Article
-
- You have access
- Export citation
On flag varieties, hyperplane complements and Springer representations of Weyl groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 3 / December 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 449-485
- Print publication:
- December 1990
-
- Article
-
- You have access
- Export citation
A character-theory-free characterization of the Mathieu group M12
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 212-230
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
Allgemeines Über Äussere Fittingpaare
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 241-249
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
The lattice of completely regular semigroup varieties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 1 / August 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 24-42
- Print publication:
- August 1990
-
- Article
-
- You have access
- Export citation
Weakly reductive semigroups with atomistic congruence lattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 1 / August 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 59-71
- Print publication:
- August 1990
-
- Article
-
- You have access
- Export citation
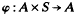 A such that (φ,1)φ and (a, st)φ = ((a, s) t)φ for all a є A and for all s, t є S. We shall refer to right
A such that (φ,1)φ and (a, st)φ = ((a, s) t)φ for all a є A and for all s, t є S. We shall refer to right 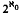 is cotorsion, is
is cotorsion, is 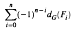 where
where 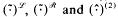 introduced in [3] have proved to be of particular interest when applied to groups. In fact, as shown in [4],
introduced in [3] have proved to be of particular interest when applied to groups. In fact, as shown in [4], 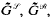
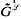 is an
is an 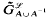 which is a subsemigroup of
which is a subsemigroup of 