The aim of this paper is to consider Problem 1 posed by Stewart and Wiegold in [6]. The main result is that if G is a finitely generated perfect group having non-trivial finite images, then there exists a finite image B of G such that the growth sequence of B is eventuallly faster than that of every finite image of G. Moreover we investigate the growth sequences of simple groups of the same order.

A closure operation connected with Hall subgroups is introduced for classes of finite soluble groups, and it is shown that this operation can be used to give a criterion for membership of certain special Fitting classes, including the so-called ‘central-socle’ classes.

We give an improved bound for the order of a p-group enjoying the title property. We also point out relations between the upper central series of a p-group and of its maximal subgroups.

A common generalization of the author's embedding theorem concerning the E-unitary regular semigroups with regular band of idempotents, and Billhardt's and Ismaeel's embedding theorem on the inverse semigroups, the closure of whose set of idempotents is a Clifford semigroup, is presented. We prove that each orthodox semigroup with a regular band of idempotents, which is an extension of an orthogroup K by a group, can be embedded into a semidirect product of an orthogroup K′ by a group, where K′ belongs to the variety of orthogroups generated by K. The proof is based on a criterion of embeddability into a semidirect product of an orthodox semigroup by a group and uses bilocality of orthogroup bivarieties.

In this paper we shall extend the classical theory of Morita equivalence to semigroups with local units. We shall use the concept of a Morita context to rediscover the Rees theorem and to characterise completely 0-simple and regular bisimple semigroups.

A number of constructions are given for arc-transitive digraphs, based on modifications of permutation representations of finite groups. In particular, it is shown that for every positive integer s and for any transitive permutation group p of degree k, there are infinitely many examples of a finite k-regular digraph with a group of automorphisms acting transitively on s-arcs (but not on (s + 1)-arcs), such that the stabilizer of a vertex induces the action of P on the out-neighbour set.

Group actions on ℝ-trees may be split into different types, and in Section 1 of this paper five distinct types are defined, with one type splitting into two sub-types. For a group G acting as a group of isometries on an ℝ-tree, conditions are considered under which a subgroup or a factor group may inherit the same type of action as G. In Section 2 subgroups of finite index are considered, and in Section 3 normal subgroups and also factor groups are considered. The results obtained here, Theorems 2.1 and 3.4, allow restrictions on possible types of actions for hypercentral, hypercyclic and hyperabelian groups to be given in Theorem 3.6. In Section 4 finitely generated subgroups are considered, and this gives rise to restrictions on possible actions for groups with certain local properties. The results throughout are stated in terms of group actions on trees. Using Chiswell's construction in [3], they could equally be stated in terms of restrictions on possible types of Lyndon length functions.

Wielandt [4] has shown that a common subnormal subgroup of two permutable subgroups of finite group is subnormal in their product. When G is infinite it seems unlikely that Wielandt's theorem will still be true, but an example illustrating this appears to be difficult, even if G is an FC-group (that is groups in which each element has only finitely many conjugates; see [2]). However, if we replace subnormality by ascendancy we have the following.

In [7] S. Pride gave a family of examples of finitely presented groups of cohomological dimension 2 having no non-trivial action on a simplicial tree. We show here that his examples have no non-trivial action on a Λ-tree, for any ordered abelian group Λ. This provides further slight evidence for an affirmative answer to Question A in §3.1 of [8]. We also give another similar family of examples.

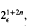If R is a 2-group of symplectic type with exponent 4, then R is isomorphic to the extraspecial group , or to the central product 4 o 2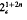1+2n of a cyclic group of order 4 and an extraspecial group, with central subgroups of order 2 amalgamated. This paper gives an explicit description of a projective representation of the group A of automorphisms of R centralizing Z(R), obtained from a faithful representation of R of degree 2n. The 2-cocycle associated with this projective representation takes values which are powers of −1 if R is isomorphic to and powers of 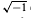otherwise. This explicit description of a projective representation is useful for computing character values or computing with central extensions of A. Such central extensions arise naturally in Aschbacher's classification of the subgroups of classical groups.

We give an alternative short proof of a recent theorem of J. A. Hillman and P.A. Linnell that an elementary amenable group with finite Hirsch number has, modulo its locally finite radical, a soluble normal subgroup with index and derived length bounded only in terms of the Hirsch number of the group.

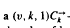A balanced directed cycle design with parameters (υ, k, 1), sometimes called a (υ, k, 1)-design, is a decomposition of the complete directed graph 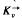into edge disjoint directed cycles of length 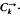k. A complete classification is given of (υ, k, 1)-designs admitting the holomorph {øa, b: x ↦ ax + b∣ a, b ∈ Zυ, (a, υ1) = 1} of the cyclic group Zυ as a group of automorphisms. In particular it is shown that such a design exists if and ony if one of (a) k = 2, (b) p ≡ 1 (mod k) for each prime p dividing υ, or (c) k is the least prime dividing υ, k2 does not divide υ, and p ≡ 1 (mod k) for each prime p < k dividing υ.

The main result of this paper is an upper bound for the number of maximal subgroups in finite solvable groups. Our result improves an earlier one of Cook, Wiegold and Williamson [1]. At the end, we use our bound to deduce an estimation for the total number of subgroups in finite solvable groups.

In this paper conditions of M-symmetry, strong, semimodularity and θ-modularity for the congruence lattice L (S) of a regular ω-semigroup S are studied. They are proved to be equivalent to modularity. Moreover it is proved that the kernel relation is a congruence on L(S) if and only if L(S) is modular, generalizing an analogous result stated by Petrich for bisimple ω-semigroups.

An existence variety of regular semigroups is a class of regular semigroups which is closed under the operations of forming all homomorphic images, all regular subsemigroups and all direct products. In this paper we generalize results on varieties of inverse semigroups to existence varieties of orthodox semigroups.

In this final contribution to the investigation of commutator laws in groups, we answer some of the questions left open in the previous two papers. The principal result is the independence of the Jacobi-Witt-Hall type laws from the so-called standard set of laws. The main results of the earlier papers are summarised. An interlude corrects some of the numerous printing errors in the second of our papers.

Band sums of associative rings were introduced by Weissglass in 1973. The main theorem claims that the support of every Artinian band sum of rings is finite. This result is analogous to the well-known theorem on Artinian semigroup rings.

We consider (finite) groups in which every two-generator subgroup has cyclic commutator subgroup. Among other things, these groups are metabelian modulo their hypercentres, and in the corresponding quotient group all subgroups of the commutator subgroup are normal.

In a well-known paper, Hall and Higman proved the reduction theorem on a coprime order operator group acting on a finite group. This theorem plays an important role in local analysis of finite group theory. In this paper, we generalize the Hall-Higman reduction theorem by dropping the restrictive hypothesis (|G|, |H|) = 1 and determine the detailed structure of G completely.

Kronecker classes of algebraci number fields were introduced by W. Jehne in an attempt to understand the extent to which the structure of an extension K: k of algebraic number fields was influenced by the decomposition of primes of k over K. He found an important link between Kronecker equivalent field extensions and a certain covering property of their Galois groups. This surveys recent contributions of Group Theory to the understanding of Kronecker equivalence of algebraic number fields. In particular some group theoretic conjectures related to the Kronecker class of an extension of bounded degree are explored.