Refine listing
Actions for selected content:
1959 results in 20xxx
The nuclear length of a character
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 49-59
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
Vertex-primitive half-transitive graphs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 113-124
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
Regular maps with small parameters
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 103-112
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
The π-character theory of solvable groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 81-102
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
Coverings and coverings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 125-128
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
Extensions of G-posets and Quillen's complex
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 60-75
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
Testing modules for irreducibility
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-16
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
The depth of the semigroup of balanced endomorphisms
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 199-208
- Print publication:
- June 1994
-
- Article
- Export citation
Metabelian Lie powers of group representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 145-168
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
Central idempotents in p-adic group rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 278-289
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
On free products of completely regular semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 212-231
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
Congruence networks for completely simple semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 243-266
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
Vertex-transitive graphs which are not Cayley graphs, I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 1 / February 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 53-63
- Print publication:
- February 1994
-
- Article
-
- You have access
- Export citation
Cusps, triangle groups and hyperbolic 3-folds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-182
- Print publication:
- October 1993
-
- Article
-
- You have access
- Export citation
On minimal Fitting classes of periodic, infinite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 3 / June 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 304-320
- Print publication:
- June 1993
-
- Article
-
- You have access
- Export citation
Congruences on free monoids and submonoids of polycyclic monoids
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 2 / April 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 236-253
- Print publication:
- April 1993
-
- Article
-
- You have access
- Export citation
Regulating hulls of almost completely decomposable groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 2 / April 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-155
- Print publication:
- April 1993
-
- Article
-
- You have access
- Export citation
On five well-known commutator identities
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 1 / February 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-19
- Print publication:
- February 1993
-
- Article
-
- You have access
- Export citation
Maximal subgroups of infinite dimensional general linear groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 3 / December 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 338-351
- Print publication:
- December 1992
-
- Article
-
- You have access
- Export citation
Finite one-relator products of two cyclic groups with the relator of arbitrary length
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 3 / December 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 352-368
- Print publication:
- December 1992
-
- Article
-
- You have access
- Export citation
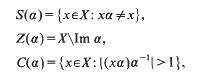
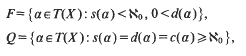
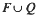 . Furthermore, both
. Furthermore, both 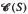 of congruences on a Rees matrix semigroup
of congruences on a Rees matrix semigroup 

