Refine listing
Actions for selected content:
1959 results in 20xxx
Enumerating p-Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 191-205
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
A group with very strange decomposition properties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 185-190
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
Free Lie algebras as modules for symmetric groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-156
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
Computation of nilpotent engel groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 214-222
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
Some challenging group presentations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 206-213
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
A recognition algorithm for non-generic classical groups over finite fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 223-253
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
Second order Dehn functions and HNN-extensions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 272-288
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
Bounds in the restricted Burnside problem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 261-271
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
Inverse semigroups with zero: covers and their structure
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 1 / August 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 15-30
- Print publication:
- August 1999
-
- Article
-
- You have access
- Export citation
On congruence compact monoids
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 205-224
- Print publication:
- June 1999
-
- Article
- Export citation
Flatness properties of acts over commutative, cancellative monoids
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 93-102
- Print publication:
- June 1999
-
- Article
- Export citation
Moore-Penrose inversion in complex contracted inverse semigroup algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-302
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
Partial characters with respect to a normal subgroup
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 104-124
- Print publication:
- February 1999
-
- Article
-
- You have access
- Export citation
Groups whose proper quotients are hypercentral
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 224-237
- Print publication:
- October 1998
-
- Article
-
- You have access
- Export citation
Dual symmetric inverse monoids and representation theory
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 3 / June 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-367
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
On groups in which every subgroup is subnormal of defect at most three
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 3 / June 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 397-420
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
Euler Characteristics and imbeddings of hyperbolic Coxeter groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-161
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
On the absence of cohomological finiteness in wreath products
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 222-230
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
Truncated tetrahedra and their reflection groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 54-72
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation
Finite groups that need more generators than any proper quotient
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 82-91
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation
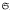 , of all permutations of a free generating set of
, of all permutations of a free generating set of 