Refine listing
Actions for selected content:
1959 results in 20xxx
Paschke's conjecture for the endpoint anisotropic series representations of the free group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 173-184
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation
Strange permutation representations of free groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 267-286
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation
Dense subsemigroups of generalised transformation semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 433-446
- Print publication:
- December 2002
-
- Article
-
- You have access
- Export citation
Strong duality for metacyclic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 377-392
- Print publication:
- December 2002
-
- Article
-
- You have access
- Export citation
Limit theorems for isotropic random walks on triangle buildings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 301-334
- Print publication:
- December 2002
-
- Article
-
- You have access
- Export citation
Bounds for nilpotent-by-finite groups in certain varieties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 393-404
- Print publication:
- December 2002
-
- Article
-
- You have access
- Export citation
Finite graphs of valency 4 and girth 4 admitting half-transitive group actions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 155-170
- Print publication:
- October 2002
-
- Article
-
- You have access
- Export citation
Metanilpotent varieties of groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 1 / August 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 55-84
- Print publication:
- August 2002
-
- Article
-
- You have access
- Export citation
Compact semilattices with open principal filters
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 349-362
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
Irreducible and end type group actions on Λ-trees
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 65-70
- Print publication:
- June 2002
-
- Article
- Export citation
The module structure of Solomon's descent algebra
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 317-334
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
Nilpotent groups are not dualizable
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 173-180
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
On the Toeplitz algebras of right-angled and finite-type Artin groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 223-246
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
Nilpotent injectors and conjugacy classes in solvable groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 3 / December 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 349-352
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
Orbit sizes, local subgroups and chains of p-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 3 / December 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 325-338
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
A syntactic approach to covers for E-dense semigroups over group varieties
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 231-245
- Print publication:
- December 2001
-
- Article
- Export citation
Torsion-free groups isomorphic to all of their non-nilpotent subgroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 3 / December 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 339-348
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
Orders in completely regular semigroups
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 213-230
- Print publication:
- December 2001
-
- Article
- Export citation
Modules over infinite nilpotent groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 211-222
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Multiplicity-free quotient tensor algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 279-298
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
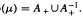 . Let λ be an endpoint of the spectrum of μ considered as a convolver on ℓ
. Let λ be an endpoint of the spectrum of μ considered as a convolver on ℓ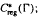 in particular, Paschke's conjecture holds for λ − μ.
in particular, Paschke's conjecture holds for λ − μ.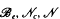 and
and 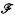 denote respectively the variety of groups of exponent dividing
denote respectively the variety of groups of exponent dividing 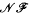 . We show that
. We show that 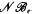 but we characterize the varieties in which that is possible. In this case, there exists a function
but we characterize the varieties in which that is possible. In this case, there exists a function 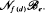 So, when
So, when 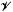 forms a variety if and only if
forms a variety if and only if 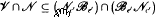 for some integers
for some integers 