Refine listing
Actions for selected content:
1959 results in 20xxx
Finite group with Hall coverings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-16
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
Homomorphisms of nonzero degree between PDn-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 335-348
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
Modular Lie representations of finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 401-424
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
Fixed Point Free Actions of Groups of Exponent 5
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-304
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
Certain relations between p-regular class sizes and the p-structure of p-solvable groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 387-400
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
Completely 0-simple semigroups of left quotients
- Part of
-
- Journal:
- Mathematika / Volume 51 / Issue 1-2 / December 2004
- Published online by Cambridge University Press:
- 26 February 2010, pp. 111-122
- Print publication:
- December 2004
-
- Article
- Export citation
On the orders of conjugacy classes in group algebras of p-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 185-190
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
On groups with all subgroups almost subnormal
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 165-174
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
Transitive simple subgroups of wreath products in product action
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 55-72
- Print publication:
- August 2004
-
- Article
-
- You have access
- Export citation
One-regular cubic graphs of order a small number times a prime or a prime square
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-356
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
C2 building and projective space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 383-402
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
Fitting classes and lattice formations II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 175-188
- Print publication:
- April 2004
-
- Article
-
- You have access
- Export citation
On Local Embedding Properties of Injectors of Finite Soluble Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 23-38
- Print publication:
- February 2004
-
- Article
-
- You have access
- Export citation
Fitting classes and lattice formations I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 93-108
- Print publication:
- February 2004
-
- Article
-
- You have access
- Export citation
On finite J-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 181-192
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
A new approach to the k(GV)-problem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 193-220
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
An Embedding Construction for Ordered Groups: To Professor Alexander Yurievich Ol'shanskii, my teacher
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 379-392
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
On The Asymptotic Values of Length Functions In Krull And Finitely Generated commutative Monoids
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 421-436
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
Group Laws Implying Virtual Nilpotence
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 295-312
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
Betti numbers of fixed point sets and multiplicities of indecomposable summands
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 165-172
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation
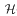 -class of
-class of 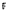 a field of
a field of 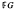 has a conjugacy class of
has a conjugacy class of 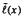 and
and 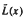 on
on 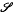 of groups including all residually or locally soluble-or-finite groups. In fact the groups of
of groups including all residually or locally soluble-or-finite groups. In fact the groups of 