Refine listing
Actions for selected content:
1959 results in 20xxx
A NOTE ON PERMUTATION GROUPS AND THEIR REGULAR SUBGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 283-287
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
De non ordinaria recognitione PSL2
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 723-734
- Print publication:
- October 2008
-
- Article
- Export citation
THE DENSITY OF SUBGROUP INDICES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 257-267
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
EMBEDDINGS OF COMPLEX LINE SYSTEMS AND FINITE REFLECTION GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 211-228
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
NATURALLY ORDERED TRANSFORMATION SEMIGROUPS PRESERVING AN EQUIVALENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 117-128
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
EMBEDDINGS IN COSET MONOIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 75-80
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
SCHREIER CONDITIONS ON CHIEF FACTORS AND RESIDUALS OF SOLVABLE-LIKE GROUP FORMATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 97-106
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
Oort groups and lifting problems
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 849-866
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
MODULAR DIOPHANTINE INEQUALITIES AND ROTATIONS OF NUMERICAL SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 315-328
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
VARIETIES GENERATED BY COMPLETELY 0-SIMPLE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 375-403
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
SEMIGROUPS OF LINEAR TRANSFORMATIONS WITH RESTRICTED RANGE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 441-453
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
Linear Groups of Finite Morley Rank
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 04 April 2008, pp. 641-651
- Print publication:
- October 2008
-
- Article
- Export citation
AUTOMORPHISMS OF METABELIAN PRIME POWER ORDER GROUPS OF MAXIMAL CLASS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 261-276
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
A PROOF OF ISBELL’S ZIGZAG THEOREM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 229-232
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
CUBIC EDGE-TRANSITIVE GRAPHS OF ORDER 8p2
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 315-323
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
RIGIDITY OF GRAPH PRODUCTS OF ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 187-196
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
FINITELY DOMINATED COVERING SPACES OF 3- AND 4-MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 99-108
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
COMMUTATIVITY DEGREES OF WREATH PRODUCTS OF FINITE ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 31-36
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
OUTER AUTOMORPHISM GROUPS OF CERTAIN TREE PRODUCTS OF ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 9-20
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
CANCELLATIVE AND MALCEV PRESENTATIONS FOR FINITE REES INDEX SUBSEMIGROUPS AND EXTENSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 39-61
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
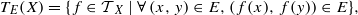
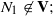 (iii)
(iii) 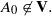 The conditions (i) and (ii) are also sufficient conditions. In this note, we complete Kublanovsky’s programme by refining condition (iii) to obtain a complete set of conditions that are both necessary and sufficient.
The conditions (i) and (ii) are also sufficient conditions. In this note, we complete Kublanovsky’s programme by refining condition (iii) to obtain a complete set of conditions that are both necessary and sufficient.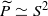 . There is a corresponding result in dimension 4, under further hypotheses on
. There is a corresponding result in dimension 4, under further hypotheses on 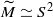 or
or 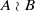 of finite Abelian groups
of finite Abelian groups 