In this article we show that finite loops with nilpotent inner mapping groups are centrally nilpotent.

The minimal faithful permutation degree μ(G) of a finite group G is the least non-negative integer n such that G embeds in the symmetric group Sym(n). Work of Johnson and Wright in the 1970s established conditions for when μ(H×K)=μ(H)+μ(K), for finite groups H and K. Wright asked whether this is true for all finite groups. A counter-example of degree 15 was provided by the referee and was added as an addendum in Wright’s paper. Here we provide two counter-examples; one of degree 12 and the other of degree 10.

We establish a link between regular subgroups of the affine group and radical circle algebras on the underlying vector space.

The arithmetic is interpreted in all the groups of Richard Thompson and Graham Higman, as well as in other groups of piecewise affine permutations of an interval which generalize the groups of Thompson and Higman. In particular, the elementary theories of all these groups are undecidable. Moreover, Thompson's group F and some of its generalizations interpret the arithmetic without parameters.

A complete Sylow sequence, 𝒫=P1,…,Pm, of a finite group G is a sequence of m Sylow pi-subgroups of G, one for each pi, where p1,…,pm are all of the distinct prime divisors of |G|. A product of the form P1⋯Pm is called a complete Sylow product of G. We prove that the solvable radical of G equals the intersection of all complete Sylow products of G if, for every composition factor S of G, and for every ordering of the prime divisors of |S|, there exist a complete Sylow sequence 𝒫 of S, and g∈S such that g is uniquely factorizable in 𝒫 . This generalizes our results in Kaplan and Levy [‘The solvable radical of Sylow factorizable groups’, Arch. Math.85(6) (2005), 490–496].

A cover of a group is a finite collection of proper subgroups whose union is the whole group. A cover is minimal if no cover of the group has fewer members. It is conjectured that a group with a minimal cover of nilpotent subgroups is soluble. It is shown that a minimal counterexample to this conjecture is almost simple and that none of a range of almost simple groups are counterexamples to the conjecture.

In 2006 we completed the proof of a five-part conjecture that was made in 1977 about a family of groups related to trivalent graphs. This family covers all 2-generator, 2-relator groups where one relator specifies that a generator is an involution and the other relator has three syllables. Our proof relies upon detailed but general computations in the groups under question. The proof is theoretical, but based upon explicit proofs produced by machine for individual cases. Here we explain how we derived the general proofs from specific cases. The conjecture essentially addressed only the finite groups in the family. Here we extend the results to infinite groups, effectively determining when members of this family of finitely presented groups are simply isomorphic to a specific quotient.

An S3-involution graph for a group G is a graph with vertex set a union of conjugacy classes of involutions of G such that two involutions are adjacent if they generate an S3-subgroup in a particular set of conjugacy classes. We investigate such graphs in general and also for the case where G=PSL(2,q).

The variety of topological groups generated by the class of all abelian kω-groups has been shown to equal the variety of topological groups generated by the free abelian topological group on [0, 1]. In this paper it is proved that the free abelian topological group on a compact Hausdorff space X generates the same variety if and only if X is not scattered.

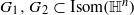J. W. Anderson (1996) asked whether two finitely generated Kleinian groups with the same set of axes are commensurable. We give some partial solutions.

This note contains some remarks on generating pairs for automorphism groups of free groups. There has been significant use of electronic assistance. Little of this is used to verify the results.

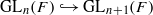Let F be an arbitrary local field. Consider the standard embedding and the two-sided action of GL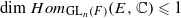n(F)×GLn(F) on GLn+1(F). In this paper we show that any GLn(F)×GLn(F)-invariant distribution on GLn+1(F) is invariant with respect to transposition. We show that this implies that the pair (GLn+1(F), GLn(F)) is a Gelfand pair. Namely, for any irreducible admissible representation (π,E) of GLn+1(F), . For the proof in the archimedean case, we develop several tools to study invariant distributions on smooth manifolds.

We consider a new subgroup In(G) in any group G of finite Morley rank. This definably characteristic subgroup is the smallest normal subgroup of G from which we can hope to build a geometry over the quotient group G/ In(G). We say that G is a geometric group if In(G) is trivial.

This paper is a discussion of a conjecture which states that every geometric group G of finite Morley rank is definably linear over a ring K1 ⊕…⊕ Kn where K1,…,Kn are some interpretable fields. This linearity conjecture seems to generalize the Cherlin–Zil'ber conjecture in a very large class of groups of finite Morley rank.

We show that, if this linearity conjecture is true, then there is a Rosenlicht theorem for groups of finite Morley rank, in the sense that the quotient group of any connected group of finite Morley rank by its hypercentre is definably linear.

We make several conjectures, and prove some results, pertaining to conjugacy classes of a given size in finite groups, especially in p-groups and 2-groups.

An enumeration result for orientably regular hypermaps of a given type with automorphism groups isomorphic to PSL(2,q) or PGL(2,q) can be extracted from a 1969 paper by Sah. We extend the investigation to orientable reflexible hypermaps and to nonorientable regular hypermaps, providing many more details about the associated computations and explicit generating sets for the associated groups.

We study Frobenius groups acting on curves.

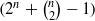We derive bivariate polynomial formulae for cocycles and coboundaries in Z2(ℤpn,ℤpn), and a basis for the (pn−1−n)-dimensional GF(pn)-space of coboundaries. When p=2 we determine a basis for the -dimensional GF(2n)-space of cocycles and show that each cocycle has a unique decomposition as a direct sum of a coboundary and a multiplicative cocycle of restricted form.

Let G be isomorphic to a group H satisfying SL(d,q)≤H≤GL(d,q) and let W be an irreducible FqG-module of dimension at most d2. We present a Las Vegas polynomial-time algorithm which takes as input W and constructs a d-dimensional projective representation of G.

We prove that a finitely generated semigroup whose word problem is a one-counter language has a linear growth function. This provides us with a very strong restriction on the structure of such a semigroup, which, in particular, yields an elementary proof of a result of Herbst, that a group with a one-counter word problem is virtually cyclic. We prove also that the word problem of a group is an intersection of finitely many one-counter languages if and only if the group is virtually abelian.

While the classification project for the simple groups of finite Morley rank is unlikely toproduce a classification of the simple groups of finite Morley rank, the enterprise has already arrived at a considerably closer approximation to that ideal goal than could have been realistically anticipated, with a mix of results of several flavors, some classificatory and others more structural, which can be combined when the stars are suitably aligned to produce results at a level of generality which, in parallel areas of group theory, would normally require either some additional geometric structure, or an explicit classification. And Bruno Poizat is generally awesome, though sometimes he goes too far.