Refine listing
Actions for selected content:
1959 results in 20xxx
DIAGRAMS OF AN ABELIAN GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 06 July 2009, pp. 38-64
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
Parabolic category O, perverse sheaves on Grassmannians, Springer fibres and Khovanov homology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 954-992
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
SELF-SMALL ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 29 June 2009, pp. 205-216
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
MAXIMAL SUBSETS OF PAIRWISE NONCOMMUTING ELEMENTS OF THREE-DIMENSIONAL GENERAL LINEAR GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 08 June 2009, pp. 91-104
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
ON p-AUTOMORPHISMS THAT ARE INNER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 08 June 2009, pp. 291-293
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
PARTIAL ACTIONS OF INVERSE AND WEAKLY LEFT E-AMPLE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 01 June 2009, pp. 355-377
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Semiclassical limits of quantum affine spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 387-407
-
- Article
-
- You have access
- Export citation
On graded centres and block cohomology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 489-514
-
- Article
-
- You have access
- Export citation
SUBGROUPS OF FINITE GROUPS WITH A STRONG COVER-AVOIDANCE PROPERTY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 499-506
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
FINITE GROUPS WITH TWO p-REGULAR CONJUGACY CLASS LENGTHS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 419-425
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
ON GENERATORS AND PRESENTATIONS OF SEMIDIRECT PRODUCTS IN INVERSE SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-365
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
A NEW CONSTRUCTION FOR REGULAR SEMIGROUPS WITH QUASI-IDEAL ORTHODOX TRANSVERSALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 177-187
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
EMBEDDING GROUPS OF CLASS TWO AND PRIME EXPONENT IN CAPABLE AND NONCAPABLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 303-308
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
GROUPS WITH COMMUTING POWERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 343-351
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
INJECTIVE TRANSFORMATIONS WITH EQUAL GAP AND DEFECT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 327-336
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
Brauer–Manin obstruction for integral points of homogeneous spaces and representation by integral quadratic forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 309-363
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
On commuting elements and embeddings of graph groups and monoids
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 155-170
-
- Article
-
- You have access
- Export citation
Endotrivial modules for the symmetric and alternating groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 45-66
-
- Article
-
- You have access
- Export citation
Hecke C*-algebras and semi-direct products
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 127-153
-
- Article
-
- You have access
- Export citation
AUTOMORPHISM GROUPS OF THE IMPRIMITIVE COMPLEX REFLECTION GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 01 February 2009, pp. 123-138
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
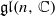 we prove that the centre of the principal block 𝒪
we prove that the centre of the principal block 𝒪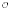
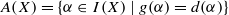 . For example, we describe Green’s relations and ideals in
. For example, we describe Green’s relations and ideals in 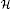 when
when 