Refine listing
Actions for selected content:
1959 results in 20xxx
CENTRES OF SYMMETRIC CELLULAR ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 14 September 2010, pp. 511-522
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
CONVEX STANDARD FUNDAMENTAL DOMAIN FOR SUBGROUPS OF HECKE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 14 September 2010, pp. 96-107
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
PRONORMALITY IN GENERALIZED FC-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 14 September 2010, pp. 220-230
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
The Alperin weight conjecture and Uno’s conjecture for the Monster 𝕄, p odd
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 27 August 2010, pp. 320-356
-
- Article
-
- You have access
- Export citation
A Satake isomorphism in characteristic p
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 23 August 2010, pp. 263-283
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
The rank of a hypergeometric system
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 17 August 2010, pp. 284-318
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
Rationality and Sylow 2-subgroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 12 August 2010, pp. 787-798
-
- Article
-
- You have access
- Export citation
Étale groupoids as germ groupoids and their base extensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 05 August 2010, pp. 765-785
-
- Article
-
- You have access
- Export citation
Independence algebras, basis algebras and semigroups of quotients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 05 August 2010, pp. 697-729
-
- Article
-
- You have access
- Export citation
Normalizers of 2-subgroups in black-box groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 307-319
-
- Article
-
- You have access
- Export citation
Approximating the Schur multiplier of certain infinitely presented groups via nilpotent quotients
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 260-271
-
- Article
-
- You have access
- Export citation
Constructing representations of Hecke algebras for complex reflection groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 426-450
-
- Article
-
- You have access
- Export citation
GROWTH OF GENERATING SETS FOR DIRECT POWERS OF CLASSICAL ALGEBRAIC STRUCTURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 21 September 2010, pp. 105-126
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
Affine Deligne–Lusztig varieties in affine flag varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 07 July 2010, pp. 1339-1382
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
FINITE GROUPS WHOSE NONCENTRAL COMMUTING ELEMENTS HAVE CENTRALIZERS OF EQUAL SIZE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 07 July 2010, pp. 293-304
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
Fundamental domains for genus-zero and genus-one congruence subgroups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 July 2010, pp. 222-245
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF LATIN RECTANGLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 167-170
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
PRESENTATION FOR RENNER MONOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 22 June 2010, pp. 30-45
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
CENTRALIZERS IN THE SEMIGROUP OF INJECTIVE TRANSFORMATIONS ON AN INFINITE SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 305-321
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
Some complements to the Lazard isomorphism
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 22 June 2010, pp. 235-262
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
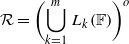
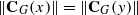 . Applying results of Schmidt [‘Zentralisatorverbände endlicher Gruppen’,
. Applying results of Schmidt [‘Zentralisatorverbände endlicher Gruppen’, 